
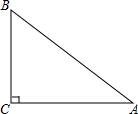
 如图,已知△ABC中,∠ACB=90°,BC=6cm,AC=8cm.
如图,已知△ABC中,∠ACB=90°,BC=6cm,AC=8cm.分析 (1)直接利用线段垂直平分线的作法得出AB的垂直平分线;
(2)利用线段垂直平分线的性质结合勾股定理以及相似三角形的判定与性质得出答案.
解答 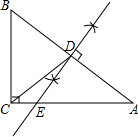 解:(1)如图所示:直线DE即为所求;
解:(1)如图所示:直线DE即为所求;
(2)∵直线DE垂直平分AB,
∴D是AB的中点,
∵∠ACB=90°,BC=6cm,AC=8cm,
∴AB=10cm,
∴CD=$\frac{1}{2}$×AB=5(cm),
∵∠A=∠A,∠ADE=∠ACB,
∴△ADE∽△ACB,
∴$\frac{AD}{AC}$=$\frac{AE}{AB}$,
则$\frac{5}{8}$=$\frac{AE}{10}$,
解得:AE=$\frac{25}{4}$(cm),
答:CD的长为5cm,AE的长为$\frac{25}{4}$cm.
点评 此题主要考查了基本作图以及相似三角形的判定与性质,得出△ADE∽△ACB是解题关键.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:选择题
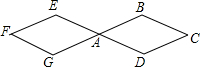 如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行.当电子甲虫爬行2015cm时停下,则它停的位置是( )
如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行.当电子甲虫爬行2015cm时停下,则它停的位置是( )| A. | 点F | B. | 点G | C. | 点A | D. | 点C |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com