
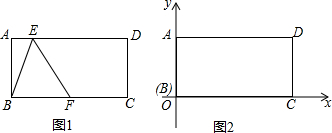
分析 如图,当点B与点D重合时,△BEF面积最大,设BE=ED=x,在RT△ABE中利用勾股定理即可解决问题.
解答 解:如图, 当点B与点D重合时,△BEF面积最大,
当点B与点D重合时,△BEF面积最大,
设BE=DE=x,则AE=4-x,
在RT△ABE中,∵EA2+AB2=BE2,
∴(4-x)2+22=x2,
∴x=$\frac{5}{2}$,
∴BE=ED=$\frac{5}{2}$,AE=AD-ED=$\frac{3}{2}$,
∴点E坐标($\frac{3}{2}$,2).
故答案为($\frac{3}{2}$,2).
点评 本题考查翻折变换、勾股定理等知识,解题的关键是理解题意,搞清楚什么时候△BFE面积最大,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 平均数 | 中位数 | 众数 | 方差 |
| 8.5 | 8.3 | 8.1 | 0.15 |
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
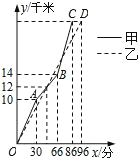 在一次自行车越野赛中,甲乙两名选手行驶的路程y(千米)随时间x(分)变化的图象(全程)如图,根据图象判定下列结论:(1)甲先到达终点;(2)前30分钟,甲在乙的前面;(3)第48分钟时,两人第一次相遇;(4)这次比赛的全程是28千米,其中正确的个数是( )
在一次自行车越野赛中,甲乙两名选手行驶的路程y(千米)随时间x(分)变化的图象(全程)如图,根据图象判定下列结论:(1)甲先到达终点;(2)前30分钟,甲在乙的前面;(3)第48分钟时,两人第一次相遇;(4)这次比赛的全程是28千米,其中正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com