Question

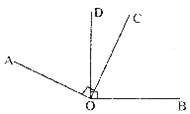
【题目】如图，若AO⊥OC，BO⊥DO，

(1)若∠DOC=38°，则∠AOB是多少度?

(2)图中有哪些角相等?

(3)若∠AOB=156°，则∠DOC是多少度?

(4)∠AOD、∠DOC、∠COB能否相等，若相等，请求出它们的度数；若不相等，说明理由．

Answer 1

【答案】(1)∠AOB=142°；

(2)∠AOC=∠BOD=90°，∠AOD=∠BOC

(3)∠DOC=24°

(4) 能相等，∠AOD=∠DOC=∠COB=45°

【解析】（1）据垂直的定义、结合图形计算即可；（2）根据直角相等、同角的余角相等解答；（3）设∠DOC=x，根据题意列方程，解方程即可；（4）设∠AOD=∠DOC=∠COB=x，结合图形列出方程，解方程即可.

解：(1)2(90°一38°)+38°=142°

(2)∠AOC=∠BOD=90° ∠AOD=∠BOC

(3)设∠DOC=，则2(90°一)+ =156°

∴=24°

(4)能相等．设∠AOD=∠DOC=∠COB=．则

90°

∴=45°.

“点睛”本题考查的是垂线的概念、余角和补角的概念。掌握垂直的定义、余角和补角的概念是解题的关键，解题时要注意运用方程思想.