
����Ŀ��ijУ��һ�δ�μ��У����������ӻ��ʽ��A���ܲ���B��������C�����٣�D����Ϸ.ȫУѧ����ѡ����һ����ʽ������С�ܶ�ͬѧ��ѡ�õĻ��ʽ����������������飬���ݵ���ͳ�ƽ���������˲�������ͳ��ͼ.


����ͳ��ͼ���ش��������⣺
��1�����ε���ѧ���� �ˣ� ![]() = ����������ͼ����������
= ����������ͼ����������
��2�������У��ѧ��2000�ˣ�������Ƹ�Уѡ�����ܲ������ֻ��ѧ��Լ�ж����ˣ�
��3��ѧУ��ÿ����A��B��C��D���ӻ��ʽ�У������ȡ���ֿ�չ���������״ͼ���б��ķ�������ÿ���ȡ��������ʽǡ�������ܲ��������������ĸ���.
���𰸡���1��300,10����ȫ����ͼ��������
��2����Уѡ���ܲ������ֻ��ѧ��Լ��800�ˣ�
��3������״ͼ��������ÿ���ȡ��������ʽǡ���ǡ��ܲ����͡��������ĸ���Ϊ![]() .
.
���������������������Ģ��ʸ�����֪������ͼ�л���������ٶ�Ӧ����ͼ����Ӧ�İٷֱȣ������������ε�������������ڴ˻��������![]() ��ֵ.����Ģ��������ġ��ܲ����İٷֱ�����Ϊ�����С��ܲ����İٷֱȣ��Դ˿��Լ������Уѡ���ܲ������ֻ��ѧ��������.����Ģ������������Żء���������ɲ�ȡ�оٷ��еĻ���״ͼ����������ע��ǡ���ǡ��ܲ����͡���������������Ӷ��������.
��ֵ.����Ģ��������ġ��ܲ����İٷֱ�����Ϊ�����С��ܲ����İٷֱȣ��Դ˿��Լ������Уѡ���ܲ������ֻ��ѧ��������.����Ģ������������Żء���������ɲ�ȡ�оٷ��еĻ���״ͼ����������ע��ǡ���ǡ��ܲ����͡���������������Ӷ��������.
�����������1����������ͼ������ͼ��֪���ܲ���������120�ˣ��ڱ������������ռ�İٷֱ�Ϊ40%��������α����������Ϊ![]() ���ˣ���
���ˣ���
������������ ![]()
![]() ���ˣ�������
���ˣ�������![]() ������
������![]() .
.
�ʷֱ�Ӧ�300��![]() ����ȫ������ͼ���£�
����ȫ������ͼ���£�
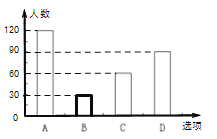
��2�������С��ܲ���������ռ������������İٷֱ�Ϊ40%�������������С��ܲ���������Ҳռ40%�����Թ��Ƹ�Уѡ���ܲ������ֻ��ѧ��Լ��![]() ���ˣ�.
���ˣ�.
��3������״ͼΪ��
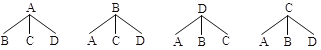
����״ͼ��֪��ÿ���ȡ��������ʽǡ���ǡ��ܲ����͡��������ĸ���![]() .
.


 �ƸԹھ��ο���ϵ�д�
�ƸԹھ��ο���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������OABC�ı߳�Ϊ6����A��C�ֱ���x�ᣬy����������ϣ���D��2��0����OA�ϣ�P��OB��һ���㣬��PA+PD����СֵΪ__��
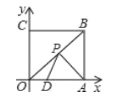
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
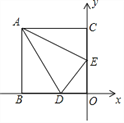
����Ŀ����֪������ABCD�У�AB��4��BC��3����M��N�ֱ��ڱ�AB��CD�ϣ�ֱ��MN�����ζԽ��� AC�ڵ�E������AME��ֱ��MN���ۣ���A���ڵ�P�����ҵ�P������CB��.
(1)��ͼ1����EP��BCʱ����CN�ij���
(2) ��ͼ2����EP��ACʱ����AM�ij���
(3) ��д���߶�CP�ij���ȡֵ��Χ������CP�ij����ʱMN�ij�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABOC�Ķ���A������Ϊ��-4��5����D��OB���е㣬E��OC�ϵ�һ�㣬����ADE���ܳ���Сʱ����E�������ǣ�������
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A��B��C�����������ϵ�λ����ͼ��ʾ�����DZ�ʾ�����ֱ���a��b��c��
��1����գ�abc�� ��0��a+b�� ��0��ab��ac�� ��0������������������������������
��2����|a|��2�ҵ�B����A��C�ľ�����ȣ�
�ٵ�b2��16ʱ����c��ֵ��
��P��������B��C����֮���һ�����㣬���P��ʾ����Ϊx����P�����˶������У�bx+cx+|x��c|��10|x+a|��ֵ���ֲ��䣬��b��ֵ��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���![]() �뷴��������
�뷴��������![]() ��ͼ���ڵ�һ���������ֱ���
��ͼ���ڵ�һ���������ֱ���![]() ��
��![]() ���㣬ֱ��
���㣬ֱ��![]() ��
��![]() �ᣬ
�ᣬ![]() ��ֱ���
��ֱ���![]() ���㣮
���㣮
��1����һ�κ����ͷ����������Ľ���ʽ��
��2���Ƚϴ�С��![]() �� ��
�� ��![]() ��
��
��3�����![]() ʱ��
ʱ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����м�������85�ˣ�ƽ��ÿ��ÿ�˿ɼӹ����ֲ���16�������ֲ���10����2�����ֲ�����3�����ֲ������һ�ף��ʼӹ��ס������ֲ��������Ŷ����˲���ʹÿ��ӹ������ֲ����պ����ף�������ӹ��˶����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���±����������Ͽ��������շѷ�ʽ.
�շѷ�ʽ | ��ʹ�÷�/Ԫ | ��ʱ����ʱ��/ | ��ʱ��/��Ԫ/ |
|
|
|
|
|
|
|
|
|
| ����ʱ |
![]() ��������ʱ��Ϊ
��������ʱ��Ϊ![]() ����ʽ
����ʽ![]() ���շѽ��ֱ�Ϊ
���շѽ��ֱ�Ϊ![]() ��ֱ��д��
��ֱ��д��![]() �Ľ���ʽ����д���Ա���
�Ľ���ʽ����д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
![]() ��գ�
��գ�![]() ������ʱ�� ʱ��ѡ��ʽ
������ʱ�� ʱ��ѡ��ʽ![]() ��ʡǮ��
��ʡǮ��
![]() ������ʱ�� ʱ��ѡ��ʽ
������ʱ�� ʱ��ѡ��ʽ![]() ��ʡǮ��
��ʡǮ��
![]() ������ʱ�� ʱ��ѡ��ʽ
������ʱ�� ʱ��ѡ��ʽ![]() ��ʡǮ��
��ʡǮ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�һ�κ���y=kx+b��k��b���dz�������k��0����ͼ���㣨1��0���ͣ�0��2����
��1������2��x��3ʱ����y��ȡֵ��Χ��
��2����֪��P��m��n���ڸú�����ͼ���ϣ���m��n=4�����P�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com