
����Ŀ����ͼ�ף�ֱ��y=��x+3��x�ᡢy��ֱ��ڵ�B����C������B��C�����������y=x2+bx+c��x�����һ������ΪA������ΪP��
��1����������ߵĽ���ʽ��
��2���ڸ������ߵĶԳ������Ƿ���ڵ�M��ʹ��C��P��MΪ�����������Ϊ���������Σ������ڣ���ֱ��д�������������ĵ�M�����ꣻ�������ڣ���˵�����ɣ�
��3����0��x��3ʱ��������������һ��E��ʹ��CBE����������ֵ��ͼ�ҡ�������ͼ̽������
���𰸡�
��1��
�⣺��ֱ��y=��x+3��x�ᡢy��ֱ��ڵ�B����C��
��B��3��0����C��0��3����
��B��C������������߽���ʽ�ɵ� ![]() �����
����� ![]() ��
��
�������߽���ʽΪy=x2��4x+3
��2��
�⣺��y=x2��4x+3=��x��2��2��1��
�������߶Գ���Ϊx=2��P��2����1����
��M��2��t������C��0��3����
��MC= ![]() =
= ![]() ��MP=|t+1|��PC=
��MP=|t+1|��PC= ![]() =2
=2 ![]() ��
��
�ߡ�CPMΪ���������Σ�
����MC=MP��MC=PC��MP=PC���������
�ٵ�MC=MPʱ������ ![]() =|t+1|�����t=
=|t+1|�����t= ![]() ����ʱM��2��
����ʱM��2�� ![]() ����
����
�ڵ�MC=PCʱ������ ![]() =2
=2 ![]() �����t=��1����P���غϣ���ȥ����t=7����ʱM��2��7����
�����t=��1����P���غϣ���ȥ����t=7����ʱM��2��7����
�۵�MP=PCʱ������|t+1|=2 ![]() �����t=��1+2
�����t=��1+2 ![]() ��t=��1��2
��t=��1��2 ![]() ����ʱM��2����1+2
����ʱM��2����1+2 ![]() ����2����1��2
����2����1��2 ![]() ����
����
���Ͽ�֪�������������ĵ�M��������Ϊ��2�� ![]() ����2��7����2����1+2
����2��7����2����1+2 ![]() ����2����1��2
����2����1��2 ![]() ��
��
��3��
�⣺��ͼ����E��EF��x�ᣬ��BC�ڵ�F����x���ڵ�D��
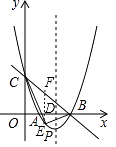
��E��x��x2��4x+3������F��x����x+3����
��0��x��3��
��EF=��x+3����x2��4x+3��=��x2+3x��
��S��CBE=S��EFC+S��EFB= ![]() EFOD+
EFOD+ ![]() EFBD=
EFBD= ![]() EFOB=
EFOB= ![]() ��3����x2+3x��=��
��3����x2+3x��=�� ![]() ��x��
��x�� ![]() ��2+
��2+ ![]() ��
��
�൱x= ![]() ʱ����CBE��������ʱE������Ϊ��
ʱ����CBE��������ʱE������Ϊ�� ![]() ����
���� ![]() ����
����
����E�������� ![]() ����
���� ![]() ��ʱ����CBE��������
��ʱ����CBE��������
����������1����ֱ�߽���ʽ�����B��C���꣬���ô���ϵ��������������߽���ʽ����2���������߽���ʽ�����P�����꼰�Գ��ᣬ�����M�����꣬��ʾ��MC��MP��PC�ij�����MC=MP��MC=PC��MP=PC����������ɷֱ�õ�����M������ķ��̣������M������ꣻ��3����E��EF��x�ᣬ��ֱ��BC�ڵ�F����x���ڵ�D�������E�����꣬��ʾ��F������꣬��ʾ��EF�ij�����һ���ɱ�ʾ����CBE����������ö��κ��������ʿ������ȡ�����ֵʱE������꣮
�����㾫����������Ĺؼ�����������κ��������ʵ����֪ʶ�����������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ǰ����Уipad�����Ѿ��ܵ����Ĺ㷺��ע��ij��ѧ��ȤС��ԡ����Ƿ�����ѧ�����ֻ���У������������������飮С�Ľ����������������²������������� Ƶ���ֲ���
���� | Ƶ�� | Ƶ�� |
�� | 5 | |
����ν | 0.1 | |
���� | 40 | 0.8 |

��1��������������˶����ˣ�����С��������ͼ������������
��2��С��Ҫ���������ݻ��Ƴ�����ͳ��ͼ��������ͼ�С��ɡ���Բ�Ľ��Ƕ��ٶȣ�
��3������У��3000��ѧ�����������Ƹ�У�֡����ԡ�̬�ȵ�ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������l���ɺ���y= ![]() �ڵ�һ�����ڵ�ͼ��������ԭ��O��ʱ����ת45��õ��ģ�����A����4
�ڵ�һ�����ڵ�ͼ��������ԭ��O��ʱ����ת45��õ��ģ�����A����4 ![]() ��4
��4 ![]() ����B��2
����B��2 ![]() ��2
��2 ![]() ����ֱ��������l�ཻ�ڵ�M��N�����OMN�����Ϊ ��
����ֱ��������l�ཻ�ڵ�M��N�����OMN�����Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����M��Բ��M����1��2������M��������ԭ��O����y�ύ�ڵ�A��������A��һ��ֱ��l����ʽΪ��y=�� ![]() x+4��x�ύ�ڵ�B����MΪ����������߾���x���ϵ�D��2��0���͵�C����4��0����
x+4��x�ύ�ڵ�B����MΪ����������߾���x���ϵ�D��2��0���͵�C����4��0����
��1���������ߵĽ���ʽ��
��2����֤��ֱ��l�ǡ�M�����ߣ�
��3����PΪ��������һ���㣬��PE��ֱ��l��ֱ������ΪE��PF��y�ᣬ��ֱ��l�ڵ�F���Ƿ���������ĵ�P��ʹ��PEF�������С�������ڣ��������ʱ��P�����꼰��PEF�������Сֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˽���꼶ѧ������������������ȡ�˾��꼶����ѧ�����е��飬����ȡѧ������������������²�������ͳ��ͼ������ͼ����ʾ�������ͼ����Ϣ�ش��������⣺ ����Ƶ���ֲ���
��� | ���أ�ǧ�ˣ� | ���� |
A | 45��x��50 | 12 |
B | 50��x��55 | m |
C | 55��x��60 | 80 |
D | 60��x��65 | 40 |
E | 65��x��70 | 16 |

��1����գ���m=��ֱ��д��������� ��������ͳ��ͼ�У�C���������ε�Բ�ĽǵĶ��������ȣ�
��2�������У���꼶��1000��ѧ�����������꼶���ص���60ǧ�˵�ѧ����Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���л�������ԴԶ�������л����֣�Ԣ����㣮Ϊ�����л����㴫ͳ�Ļ���ijУ��ί��֯��һ��ȫУ3000��ѧ���μӵġ�������д��������Ϊ�˽Ȿ�δ����ijɼ���У��ί�����ȡ������200��ѧ���ijɼ���Ϊ��������ͳ�ƣ��Ƴ����²�������ͳ��ͼ����
Ƶ��Ƶ�ʷֲ���
�ɼ�x���֣� | Ƶ�����ˣ� | Ƶ�� |
50��x��60 | 10 | 0.05 |
60��x��70 | 30 | 0.15 |
70��x��80 | 40 | n |
80��x��90 | m | 0.35 |
90��x��100 | 50 | 0.25 |
����������Ϣ������������⣺
��1��m= �� n=��
��2����ȫƵ���ֲ�ֱ��ͼ��
��3����200��ѧ���ɼ�����λ�������������Σ�
��4�����ɼ���90�����ϣ�����90�֣�Ϊ���š��ȣ�������Ƹ�У�μӱ��α�����3000��ѧ���гɼ��ǡ��š��ȵ�Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�͡�DEF������ȫ�ȵĵ���ֱ�������Σ���BAC=��EDF=90�㣬��DEF�Ķ���E���ABC��б��BC���е��غϣ�����DEF�Ƶ�E��ת����ת�����У��߶�DE���߶�AB�ཻ�ڵ�P���߶�EF������CA�ཻ�ڵ�Q�� 
��1����ͼ�٣�����Q���߶�AC�ϣ���AP=AQʱ����֤����BPE�ա�CQE��
��2����ͼ�ڣ�����Q���߶�CA���ӳ�����ʱ����֤����BPE�ס�CEQ������BP=2��CQ=9ʱBC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ABCD�У�AD��BC����B=90�㣬AG��CD��BC�ڵ�G����E��F�ֱ�ΪAG��CD���е㣬����DE��FG�� 
��1����֤���ı���DEGF��ƽ���ı��Σ�
��2������G��BC���е�ʱ����֤���ı���DEGF�����Σ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com