
| A. | $\sqrt{2x+3}$+4=0 | B. | $\sqrt{x-7}$+$\sqrt{x}$=7 | C. | $\sqrt{x-3}$=1-x | D. | $\sqrt{x-1}$+$\sqrt{1-x}$=3 |
分析 根据二次根式必须有意义,可以得到选项中的无理方程是否有解,从而可以解答本题.
解答 解:∵$\sqrt{2x+3}+4=0$,
∴$\sqrt{2x+3}=-4$,
∵$\sqrt{2x+3}≥0$,
∴$\sqrt{2x+3}+4=0$无解;
∵$\sqrt{x-7}+\sqrt{x}=7$,
∴x-7≥0,且x≥0,
∴x≥7,
∴$\sqrt{x-7}+\sqrt{x}=7$有解;
∵$\sqrt{x-3}=1-x$,
∴x-3≥0得x≥3,则1-x<0,
∴$\sqrt{x-3}=1-x$无解;
∵$\sqrt{x-1}+\sqrt{1-x}=3$,
∴x-1≥0且1-x≥0,
得x=1,
∴$\sqrt{x-1}+\sqrt{1-x}=0$,
∴$\sqrt{x-1}+\sqrt{1-x}=3$无解;
故选B.
点评 本题考查无理方程,解题的关键是明确无理方程首先要保证根号里的式子有意义.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
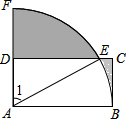 如图,在矩形ABCD中,AB=4,BC=2,以A为圆心,AB的长为半径画弧,交DC于点E,交AD延长线于点F,则图中阴影部分的面积为8-4$\sqrt{3}$+$\frac{4}{3}$π.
如图,在矩形ABCD中,AB=4,BC=2,以A为圆心,AB的长为半径画弧,交DC于点E,交AD延长线于点F,则图中阴影部分的面积为8-4$\sqrt{3}$+$\frac{4}{3}$π.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
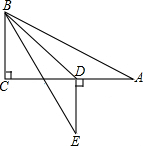 如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=8,点D在AC边上,将△ABD沿着BD翻折后,点A落在点E处,如果AD⊥DE、那么DE的长度为4$\sqrt{3}-4$.
如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=8,点D在AC边上,将△ABD沿着BD翻折后,点A落在点E处,如果AD⊥DE、那么DE的长度为4$\sqrt{3}-4$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知一次函数y=kx+b的图象与直线y=2x-$\sqrt{3}$平行,它与x轴、y轴分别相交于点A、B;它在y轴上的截距是4.平面直角坐标系的坐标原点为O.
已知一次函数y=kx+b的图象与直线y=2x-$\sqrt{3}$平行,它与x轴、y轴分别相交于点A、B;它在y轴上的截距是4.平面直角坐标系的坐标原点为O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com