Question

1．如图，△ABC为等边三角形，P为AB上一点，PE⊥BC于E交AC于F，在BC的延长线上截取CD=PA，PD交AC于I，$\frac{PA}{PB}=n$．
（1）如图1，当n=1时，$\frac{EC}{CD}$=$\frac{3}{2}$，$\frac{FI}{ED}$=1．（直接写出）
（2）如图2，∠EPD=60°，并求出$\frac{FI}{ED}$的值，请写出证明的过程．
（3）如图3，当P在AB延长线上，其它条件不变，当n=3时，$\frac{EC}{CD}$=$\frac{5}{6}$．（直接写出）

Answer 1

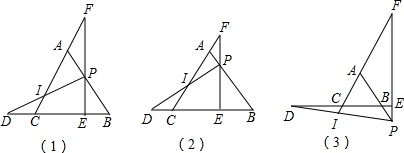
分析 （1）①由题意，在直角△CEF中，∠F=30°，则CE=$\frac{1}{2}$CF，又由∠BAC=∠F+∠APF=60°，可得AF=AP=CD=$\frac{1}{2}$AB，CD=$\frac{1}{3}$CF，即可得出；
②如图1，作PG∥BC，IH∥BC，可得IH=$\frac{1}{2}$FI，易证△PGI≌△DCI，则DI=PI，在△PDE中，IH是中位线，可得IH=$\frac{1}{2}$DE，即可得出；
（2）连BP，且过P作PM⊥AC于M，过P点作PN∥BC交AC于N，可得△ANP为等边三角形，证△PNI≌△DCI，根据等边三角形的性质和全等三角形的性质得CI=CD，即可求出n的值；在△AMP中可得AM=$\frac{1}{2}$an，CM=a+$\frac{1}{2}$an，CE=$\frac{1}{2}$a+an，由∠EPB=∠APF=30°，可得AF=AP=an，FI=2an+$\frac{1}{2}$a，即可求出；
（3）根据（1）的推理原理，即可推出结果．

解答 解：（1）①∵等边三角形ABC，
∴∠ABC=∠ACB=∠BAC=60°，AB=AC=BC，
∵EF⊥BC，
∴在直角△CEF中，∠F=30°，
∴CE=$\frac{1}{2}$CF，
∵PA=nPB，n=1，
∴2PA=AC，
又∵∠BAC=∠F+∠APF=60°，
∴AF=AP=CD=$\frac{1}{2}$AC，
∴CD=$\frac{1}{3}$CF，
∵CE=$\frac{1}{2}$CF，
∴$\frac{EC}{CD}=\frac{3}{2}$；
②如图1，作PG∥BC，IH∥BC，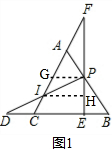

∴IH=$\frac{1}{2}$FI，
易证△PGI≌△DBI，则DI=PI，
∴在△PDE中，IH是中位线，
∴IH=$\frac{1}{2}$DE，
∴$\frac{FI}{ED}$=1；
（2）如图2，设PB=a，则PA=an；连CP，且过P作PM⊥AC于M；

过P点作PN∥BC交AC于N，
可△ANP为等边三角形，
所以AP=PN=AN，
∴△PNI≌△DCI（AAS），
∴IB=$\frac{1}{2}$a，
又∵∠PED=90°，
∴∠D=∠CID=30°，
∴CI=CD，即$\frac{1}{2}a$=an，
∴n=$\frac{1}{2}$，
在△AMP中可得AM=$\frac{1}{2}$an，
∴CM=a+an-$\frac{1}{2}$an=a+$\frac{1}{2}$an，
CE=a+an-$\frac{1}{2}$a=$\frac{1}{2}$a+an，
又∵DC=PA，
∴DE=$\frac{1}{2}$a+an+an=2an+$\frac{1}{2}$a，
又∵∠EPB=∠APF=30°，
而∠BAF=120°，∠F=30°，
∴AF=AP=an，
∴FI=2an+$\frac{1}{2}$a，
∴$\frac{FI}{ED}=\frac{2an+\frac{1}{2}a}{2an+\frac{1}{2}a}$=1；
（3）∵等边三角形ABC，
∴∠ABC=∠ACB=∠BAC=60°，AB=AC=BC，
∵EF⊥BC，
∴在直角△CEF中，∠F=30°，
∴CE=$\frac{1}{2}$CF，
∵PA=nPC，n=3，
∴PA=$\frac{2}{3}$AB，
又∵∠BAC=∠F+∠APF=60°，
∴AF=AP=CD=$\frac{2}{3}$AB，
∴CD=$\frac{5}{3}$CF，
∵CE=$\frac{1}{2}$CF，
∴$\frac{EC}{CD}$=$\frac{5}{6}$．
故答案为：（1）$\frac{3}{2}$，1；（3）$\frac{5}{6}$．

点评 本题主要考查相似三角形的判定与性质、等边三角形性质、中位线定理、直角三角形性质等知识点，综合程度大，根据题意通过全等等知识表示出线段的长得出比值是根本思路．