
分析 (1)将M、N展开并做差,即可得出M-N=-6x,根据x的取值范围即可得出M、N之间的大小关系;
(2)根据提价方案求出提价后三种方案的价格,做差后可得出方案3提价最多.
解答 解:(1)∵M=(x-2)(x-16)=x2-18x+32,N=(x-4)(x-8)=x2-12x+32,
∴M-N=(x2-18x+32)-(x2-12x+32)=-6x,
∴当x>0时,-6x<0,M<N;
当x=0时,-6x=0,M=N;
当x<0时,-6x>0,M>N.
(2)方案1:a(1+p%)(1+q%);
方案2:a(1+p%)(1+q%);
方案3:a(1+$\frac{p+q}{2}$%)2.
设p%=m,q%=n,则提价后三种方案的价格分别为:
方案1:a(1+m)(1+n)=a(1+m+n+mn);
方案2:a(1+m)(1+n)=a(1+m+n+mn);
方案3:a(1+$\frac{m+n}{2}$)2=a(1+m+n+$\frac{{m}^{2}+2mn+{n}^{2}}{4}$).
a(1+m+n+$\frac{{m}^{2}+2mn+{n}^{2}}{4}$)-a(1+m+n+mn),
=a(1+m+n+$\frac{{m}^{2}+2mn+{n}^{2}}{4}$-1-m-n-mn),
=a($\frac{{m}^{2}+2mn+{n}^{2}}{4}$-mn),
=$\frac{a}{4}$(m-n)2,
∵p≠q,
∴m≠n,
∴$\frac{a}{4}$(m-n)2>0,
∴方案3提价最多.
故答案为:a(1+p%)(1+q%);a(1+p%)(1+q%);a(1+$\frac{p+q}{2}$%)2.
点评 本题考查了因式分解的应用,解题的关键是:(1)做差后得出M-N=-6x;(2)做差后得出方案3提价最多.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
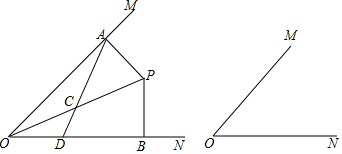
 为整治城市街道的汽车超速现象,交警大队在某街道旁进行了流动测速.如图,一辆小汽车在某城市街道上直行,某一时刻刚好行驶到离车速检测仪A60m的C处,过了4s后,小汽车到达离车速检测仪A100m的B处,已知该段城市街道的限速为60km/h,请问这辆小汽车是否超速?
为整治城市街道的汽车超速现象,交警大队在某街道旁进行了流动测速.如图,一辆小汽车在某城市街道上直行,某一时刻刚好行驶到离车速检测仪A60m的C处,过了4s后,小汽车到达离车速检测仪A100m的B处,已知该段城市街道的限速为60km/h,请问这辆小汽车是否超速?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 投掷一枚均匀的硬币100次,正面朝上的次数为50次 | |
| B. | 任意一个一元二次方程都有实数根 | |
| C. | 三角形的外心在三角形的外部 | |
| D. | 直角三角形的形斜边上的中线等于斜边的一般 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
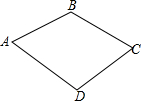 如图,在四边形ABCD中,点D在线段AB、BC的垂直平分线上,若∠D=110°,则∠B度数为( )
如图,在四边形ABCD中,点D在线段AB、BC的垂直平分线上,若∠D=110°,则∠B度数为( )| A. | 110° | B. | 115° | C. | 120° | D. | 125° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
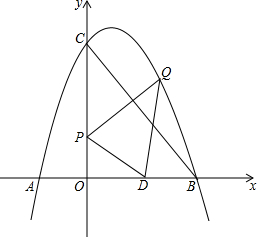 已知抛物线y=$-\frac{1}{3}{x}^{2}+\frac{5}{3}x+12$与x轴交于点A,B(A在B的左侧),与y轴交于点C,连接BC,y轴上的点P(0,m),过点P作BC的垂线交对称轴右侧抛物线于点Q,D为x轴上一动点.
已知抛物线y=$-\frac{1}{3}{x}^{2}+\frac{5}{3}x+12$与x轴交于点A,B(A在B的左侧),与y轴交于点C,连接BC,y轴上的点P(0,m),过点P作BC的垂线交对称轴右侧抛物线于点Q,D为x轴上一动点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com