
【题目】“一带一路”的战略构想为国内许多企业的发展带来了新的机遇,某公司生产A,B两种机械设备,每台B种设备的成本是A种设备的1.5倍,公司若投入16万元生产A种设备,36万元生产B种设备,则可生产两种设备共10台.请解答下列问题:
(1)A、B两种设备每台的成本分别是多少万元?
(2)若A,B两种设备每台的售价分别是6万元,10万元,公司决定生产两种设备共60台,计划销售后获利不低于126万元,且A种设备至少生产53台,求该公司有几种生产方案;
(3)在(2)的条件下,销售前公司决定从这批设备中拿出一部分,赠送给“一带一路”沿线的甲国,剩余设备全部售出,公司仍获利44万元,赠送的设备采用水路运输和航空运输两种方式,共运输4次,水路运输每次运4台A种设备,航空运输每次运2台B种设备(运输过程中产生的费用由甲国承担).直接写出水路运输的次数.
【答案】(1)A种设备每台的成本是4万元,B种设备每台的成本是6万元.(2)该公司有5种生产方案.(3)水路运输的次数为2次.
【解析】分析:(1)设A种设备每台的成本是x万元,B种设备每台的成本是1.5x万元.根据数量=总价÷单价结合“投入16万元生产A种设备,36万元生产B种设备,则可生产两种设备共10台”,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)设A种设备生产a台,则B种设备生产(60-a)台.根据销售后获利不低于126万元且A种设备至少生产53台,即可得出关于a的一元一次不等式组,解之即可得出a的取值范围,再根据a为正整数即可得出a的值,进而即可得出该公司生产方案种数;
(3)设水路运输了m次,则航空运输(4-m)次,该公司赠送4m台A种设备,(8-2m)台B种设备,根据利润=销售收入-成本结合公司获利44万元,即可得出关于a、m的二元一次方程,根据a、m的取值范围结合a、m均为正整数,再代入m值验证生产的B种设备是否低于赠送的B种设备,由此即可得出结论.
详解:(1)设A种设备每台的成本是x万元,B种设备每台的成本是1.5x万元.
根据题意得:![]() ,
,
解得:x=4,
经检验x=4是分式方程的解,
∴1.5x=6.
答:A种设备每台的成本是4万元,B种设备每台的成本是6万元.
(2)设A种设备生产a台,则B种设备生产(60-a)台.
根据题意得:![]() ,
,
解得:53≤a≤57.
∵a为整数,
∴a=53,54,55,56,57,
∴该公司有5种生产方案.
(3)设水路运输了m次,则航空运输(4-m)次,该公司赠送4m台A种设备,(8-2m)台B种设备,
根据题意得:6(a-4m)+10[60-a-(8-2m)]-4a-6(60-a)=44,
整理得:a+2m-58=0,
解得:m=29-![]() a.
a.
∵53≤a≤57,0<m<4,且a、m均为正整数,
∴m=1或2.
当m=1时,a=56,
∴60-a=4,8-2m=6.
∵4<6,
∴m=1不合适,舍去;
当m=2时,a=54,
∴60-a=6,8-2m=4.
∵6>4,
∴m=2符合题意.
∴水路运输的次数为2次.


科目:初中数学 来源: 题型:
【题目】如图,直线y=3x与反比例函数y=![]() (k≠0)的图象交于A(1,m)和点B.
(k≠0)的图象交于A(1,m)和点B.

(1)求m,k的值,并直接写出点B的坐标;
(2)过点P(t,0)(-1≤t≤1)作x轴的垂线分别交直线y=3x与反比函数y=![]() (k≠0)的图象于点E,F.
(k≠0)的图象于点E,F.
①当t=![]() 时,求线段EF的长;
时,求线段EF的长;
②若0<EF≤8,请根据图象直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,俄罗斯方块游戏中,图形![]() 经过平移使其填补空位,则正确的平移方式是( )
经过平移使其填补空位,则正确的平移方式是( )
[Failed to download image : http://192.168.0.10:8086/QBM/2019/8/9/2265110730670080/2266396395864065/STEM/34cd169bb880437797498d7a59a34864.png]
A.先向右平移5格,再向下平移3格
B.先向右平移4格,再向下平移5格
C.先向右平移4格,再向下平移4格
D.先向右平移3格,再向下平移5格
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线a // b,点A、E在直线a上,点B、F在直线b上,∠ABC=100°,BD平分∠ABC交直线a于点D,线段EF在线段AB的左侧.若将线段EF沿射线 AD的方向平移,在平移的过程中BD所在的直线与 EF所在的直线交于点P.试探索 ∠1的度数与∠EPB的度数有怎样的关系?

为了解决以上问题,我们不妨从EF的某些特殊位置研究,最后再进行一般化.
(特殊化)
(1)如图,当∠1=40°,且点P在直线a、b之间时,求∠EPB的度数;

(2)当∠1=70 °时,求∠EPB的度数;

(一般化)
(3)当∠1=n°时,求∠EPB的度数.(直接用含n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A、B、C、D四个整数点![]() 即各点均表示整数
即各点均表示整数![]() ,且
,且![]() ,若A、D两点表示的数的分别为
,若A、D两点表示的数的分别为![]() 和6,点E为BD的中点,那么该数轴上上述五个点所表示的整数中,离线段BD的中点最近的整数是
和6,点E为BD的中点,那么该数轴上上述五个点所表示的整数中,离线段BD的中点最近的整数是![]()
![]()
![]()
A. ![]() B. 0C. 1D. 2
B. 0C. 1D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD为矩形,![]() ,
,![]() ,点E是CD的中点,点P在AB上以每秒2个单位的速度由A向B运动,设运动时间为t秒.
,点E是CD的中点,点P在AB上以每秒2个单位的速度由A向B运动,设运动时间为t秒.

(1)当点P在线段AB上运动了t秒时,![]() __________________(用代数式表示);
__________________(用代数式表示);
(2)t为何值时,四边形PDEB是平行四边形:
(3)在直线AB上是否存在点Q,使以D、E、Q、P四点为顶点的四边形是菱形?若存在,求出t的值:若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
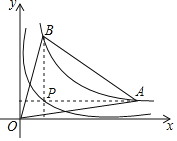
【题目】如图,点P为函数y=![]() (x>0)图象上一点,过点P作x轴、y轴的平行线,分别与函数y=
(x>0)图象上一点,过点P作x轴、y轴的平行线,分别与函数y=![]() (x>0)的图象交于点A、B,则△AOB的面积为_____.
(x>0)的图象交于点A、B,则△AOB的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生在一次射击训练中,随机抽取10名学生的成绩如下表,请回答问题:
环数 | 6 | 7 | 8 | 9 |
人数 | 1 | 5 | 2 |
(1)填空:10名学生的射击成绩的众数是 ,中位数是 .
(2)求这10名学生的平均成绩.
(3)若9环(含9环)以上评为优秀射手,试估计全年级500名学生中有多少是优秀射手?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】青岛市某大酒店豪华间实行淡季、旺季两种价格标准,旺季每间比淡季上涨![]() ,下表是去年该酒店豪华间某两天的相关记录:
,下表是去年该酒店豪华间某两天的相关记录:
旺季 | 淡季 | |
未入住房间数 | 10 | 0 |
日总收入(元) | 24 000 | 40 000 |
(1)该酒店豪华间有多少间?旺季每间价格为多少元
(2)今年旺季来临,豪华间的间数不变。经市场调查发现,如果豪华间仍旧实行去年旺季价格,那么每天都客满;如果价格继续上涨,那么每增加25元,每天未入住房间数增加1间。不考虑其他因素,该酒店将豪华间的价格上涨多少元时,豪华间的日总收入最高?最高日总收入是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com