Question

【题目】如图，已知直线a // b，点A、E在直线a上，点B、F在直线b上，∠ABC＝100°，BD平分∠ABC交直线a于点D，线段EF在线段AB的左侧.若将线段EF沿射线 AD的方向平移，在平移的过程中BD所在的直线与 EF所在的直线交于点P．试探索 ∠1的度数与∠EPB的度数有怎样的关系？

为了解决以上问题，我们不妨从EF的某些特殊位置研究，最后再进行一般化.

（特殊化）

（1）如图，当∠1＝40°，且点P在直线a、b之间时，求∠EPB的度数；

（2）当∠1＝70 °时，求∠EPB的度数；

（一般化）

（3）当∠1＝n°时，求∠EPB的度数.（直接用含n的代数式表示）

Answer 1

【答案】（1）170°（2）见解析（3）①见解析②见解析

【解析】

（1）作PG∥a，根据平行线性质和角平分线性质可得∠GPB=180°－∠ABC=130°，计算即可；（2）作PG∥a，结合画图，分3种情况当交点P在直线a上方，∠EPB＝20°；当交点P在直线a、b之间，∠EPB＝160°；当交点P在直线b下方，∠EPB＝20°；（3）根据（1）（2）情况，分2种情况①当n＞50°时；②当n＜50°时，各有3种情况.

（1）作PG∥a，

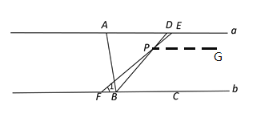
∴∠EPG＝∠EFC=400

∵a∥b

∴PG∥b

∴∠GPB＋∠CBD=1800

又∵BD是∠ABC平分线，且∠ABC=1000，

∴∠GPB=1800－∠ABC=1300

∴∠EPB＝∠EPG＋∠GPB=1700

（2）①当交点P在直线a上方，作PG∥a，

∵a∥b

∴PG∥b

∴∠EPG=∠1, ∠GPB=∠DBC

∴∠EPB＝700－500=200

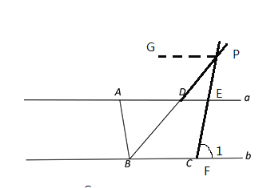
②当交点P在直线a、b之间，作PG∥a，

∵a∥b

∴PG∥b

∴∠GPB=∠PBC=∠ABC=500,∠BFE＝∠EPG=1800-∠1

∴∠EPB＝∠EPG＋∠GPB=500+1800-∠1=2300－700=1600

③当交点P在直线b下方，作PG∥a，

∵a∥b

∴PG∥b

∴∠EPG=∠1, ∠GPB=∠DBC

∴∠EPB＝700－500=200

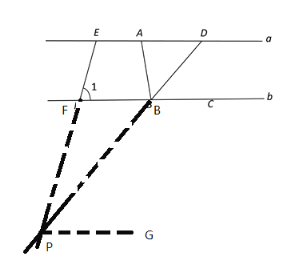
（3）由（1）（2）得：①当n＞500时，

交点P在直线a上方，∠EPB＝n－500

交点P在直线a、b之间，∠EPB＝2300－n

交点P在直线b下方，∠EPB＝n－500

②当n＜500时，

交点P在直线a上方，∠EPB＝500－n

交点P在直线a、b之间，∠EPB＝1300＋n

交点P在直线b下方，∠EPB＝500－n