
【题目】观察下列等式:
![]() =1﹣
=1﹣![]() ,
,![]() ;
;![]() ,……,
,……,
将以上二个等式两边分别相加得:
![]() ++
++![]() +
+![]() =1﹣
=1﹣![]() +
+![]() ﹣
﹣![]() +
+![]() ﹣
﹣![]() =
=![]()
用你发现的规律解答下列问题:
(1)直接写出下列各式的计算结果:
①![]() +
+![]() +
+![]() +…+
+…+![]() = ;
= ;
②![]() +
+![]() +
+![]() +…+
+…+![]() = ;
= ;
(2)仿照题中的计算形式,猜想并写出:![]() = ;
= ;
(3)解方程:![]() +
+![]() +
+![]() =
=![]() .
.
科目:初中数学 来源: 题型:
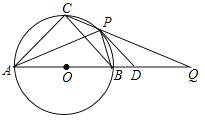
【题目】如图,等腰△ABC三个顶点在⊙O上,直径AB=12,P为弧BC上任意一点(不与B,C重合),直线CP交AB延长线与点Q,2∠PAB+∠PDA=90°,下列结论:①若∠PAB=30°,则弧BP的长为![]() ;②若PD//BC,则AP平分∠CAB;③若PB=BD,则
;②若PD//BC,则AP平分∠CAB;③若PB=BD,则![]() ,④无论点P在弧
,④无论点P在弧![]() 上的位置如何变化,CP·CQ为定值. 正确的是___________.
上的位置如何变化,CP·CQ为定值. 正确的是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线a // b,点A、E在直线a上,点B、F在直线b上,∠ABC=100°,BD平分∠ABC交直线a于点D,线段EF在线段AB的左侧.若将线段EF沿射线 AD的方向平移,在平移的过程中BD所在的直线与 EF所在的直线交于点P.试探索 ∠1的度数与∠EPB的度数有怎样的关系?

为了解决以上问题,我们不妨从EF的某些特殊位置研究,最后再进行一般化.
(特殊化)
(1)如图,当∠1=40°,且点P在直线a、b之间时,求∠EPB的度数;

(2)当∠1=70 °时,求∠EPB的度数;

(一般化)
(3)当∠1=n°时,求∠EPB的度数.(直接用含n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD为矩形,![]() ,
,![]() ,点E是CD的中点,点P在AB上以每秒2个单位的速度由A向B运动,设运动时间为t秒.
,点E是CD的中点,点P在AB上以每秒2个单位的速度由A向B运动,设运动时间为t秒.

(1)当点P在线段AB上运动了t秒时,![]() __________________(用代数式表示);
__________________(用代数式表示);
(2)t为何值时,四边形PDEB是平行四边形:
(3)在直线AB上是否存在点Q,使以D、E、Q、P四点为顶点的四边形是菱形?若存在,求出t的值:若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
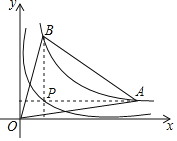
【题目】如图,点P为函数y=![]() (x>0)图象上一点,过点P作x轴、y轴的平行线,分别与函数y=
(x>0)图象上一点,过点P作x轴、y轴的平行线,分别与函数y=![]() (x>0)的图象交于点A、B,则△AOB的面积为_____.
(x>0)的图象交于点A、B,则△AOB的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生在一次射击训练中,随机抽取10名学生的成绩如下表,请回答问题:
环数 | 6 | 7 | 8 | 9 |
人数 | 1 | 5 | 2 |
(1)填空:10名学生的射击成绩的众数是 ,中位数是 .
(2)求这10名学生的平均成绩.
(3)若9环(含9环)以上评为优秀射手,试估计全年级500名学生中有多少是优秀射手?
查看答案和解析>>
科目:初中数学 来源: 题型:
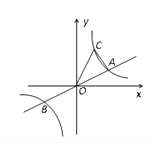
【题目】如图,已知直线![]() 与双曲线y=
与双曲线y=![]() 交于A、B两点,点B的坐标为(-4,-2),C为第一象限内双曲线y=
交于A、B两点,点B的坐标为(-4,-2),C为第一象限内双曲线y=![]() 上一点,且点C在直线
上一点,且点C在直线![]() 的上方.
的上方.
(1)求双曲线的函数解析式;
(2)若△AOC的面积为6,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() (x>0)的图象交于A(2,﹣1)、B(
(x>0)的图象交于A(2,﹣1)、B(![]() ,n)两点.直线y=2与y轴交于点C.
,n)两点.直线y=2与y轴交于点C.
1)求一次函数与反比例函数的解析式;
2)求△ABC的面积;
3)直接写出不等式kx+b>![]() 在如图所示范围内的解集.
在如图所示范围内的解集.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com