【题目】李欣同学下午5：30放学离校，此刻时钟上时针与分针的夹角大小应为________ ．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】武汉开发区一初中官士墩校区前期建设投入约153000000元．数据153000000用科学记数法可表示为_________________ ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】【知识生成】我们已经知道，通过不同的方法表示同一图形的面积，可以探求相应的等式.
2002年8月在北京召开了国际数学大会，大会会标如图1所示，它是由四个形状大小完全相同的直角三角形与中间的小正方形拼成的一个大正方形.直角三角形的两条直角边长分别为a、b ,斜边长为c.
（1）图中阴影部分的面积用两种方法可分别表示为 、 ；
（2）你能得出的a, b, c之间的数量关系是 （等号两边需化为最简形式）；
（3）若一直角三角形的两条直角边长为5和12, 则其斜边长为 .
【知识迁移】通过不同的方法表示同一几何体的体积，也可以探求相应的等式.
如图2是边长为
的正方体，被如图所示的分割线分成8块.
（4）用不同的方法计算这个正方体的体积，就可以得到一个等式，这个等式可以为 ；
（5）已知
, 
,利用上面的规律求
的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将平行四边形纸片ABCD按如图方式折叠，使点C与点A重合，点D落到D’处，折痕为EF.
(1)、求证：△ABE≌△AD’F;
(2)、连接CF,判断四边形AECF是否为平行四边形？请证明你的结论。
(3)、若AE=5，求四边形AECF的周长。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某店出售甲、乙、丙三种不同型号的电动车，已知甲型车的第一季度销售额占这三种车总销售额的56%，第二季度乙、丙两种型号车的销售额比第一季度减少了a%，但该商场电动车的总销售额比第一季度增加了12%，且甲型车的销售额比第一季度增加了23%，则a的值为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
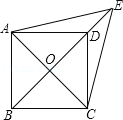
【题目】如图，已知平行四边形ABCD中，对角线AC，BD交于点O，E是BD延长线上的点，且△ACE是等边三角形．
（1）求证：四边形ABCD是菱形；
（2）若∠AED=2∠EAD，求证：四边形ABCD是正方形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读理解：配方法是中学数学的重要方法，用配方法可求最大（小）值。如对于任意正实数
、x，可作变形：x+=(－
)2+2，因为(－)2≥0，所以x+≥2（当x=时取等号）．
记函数y=x+（a＞0，x＞0），由上述结论可知：当x=时，该函数有最小值为2．
直接应用： 已知函数y1=x（x＞0）与函数y2 = （x＞0），则当x= 时，y1+y2取得最小值为 ．
变形应用： 已知函数y1=x+1（x＞-1）与函数y2=（x+1）2+4（x＞-1），求 的最小值，并指出取得该最小值时相应的x的值．
实际应用：汽车的经济时速是指汽车最省油的行驶速度。某种汽车在每小时70～110公里之间行驶时（含70公里和110公里），每公里耗油（+）升。若该汽车以每小时x公里的速度匀速行驶，1小时的耗油量为y升．
①、求y关于x的函数关系式（写出自变量x的取值范围）；
②、求该汽车的经济时速及经济时速的百公里耗油量（结果保留小数点后一位）．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
