Question

【题目】如图，在菱形ABCD中，E、F分别是AB和BC上的点，且BE=BF．

（1）求证：△ADE≌△CDF；
（2）若∠A=40°，∠DEF=65°，求∠DFC的度数．

Answer 1

【答案】
（1）解：∵四边形ABCD是菱形，

∴∠A=∠C，AB=CB，AD=DC，

∵BE=BF，

∴AE=CF，

在△ADE和△CDF中，

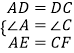
∴△ADE≌△CDF

（2）解：∵△ADE≌△CDF，

∴DE=DF，

∵∠DEF=65°，

∴∠EDB=∠FDB=25°，

∵四边形ABCD是菱形，

∴AB=AD，

∵∠A=40°，

∴∠ADB=70°，

∴∠ADE=70°﹣25°=45°，

∴∠DFC=180°﹣40°﹣45°=95°

【解析】（1）根据菱形的性质和全等三角形的判定方法“SAS”即可证明△ADE≌△CDF；（2）根据△ADE≌△CDF，得到DE=DF，再求出∠EDB=∠FDB=25°，根据四边形ABCD是菱形，∠A=40°，求出∠ADB=70°，∠ADE=45°，再根据三角形的内角和为180°，即可解答．
【考点精析】关于本题考查的菱形的性质，需要了解菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半才能得出正确答案．