
解:(1)连接BD.(如图1)
∵四边形ABCD是矩形,
∴AD⊥PB.
∴∠PAD=∠BAD=90°.△PAD与△ABD都是直角三角形.
∵PD=15,PA=9,
∴AD=12.
∵DP切⊙O于D,
∴BD⊥DP.
∴∠PDB=90°.
∵∠P+∠ADP=∠ADP+∠ADB=90°,
∴∠P=∠ADB.
∵tan∠P=

=

=

,
∴tan∠ADB=

=

.
∴AB=AD•tan∠ADB=

=16;
(2)(如图2)
∵过点E作直线EF,交PB于点F,并将四边形PBCD的周长平分,
AB=16,AD=12,
∴四边形PBCD的周长为:15+16+12+16+9=68,

∴PE+PF=34,
∵PE=x,
∴PF=34-x,
EN=PE•sin∠P=

x.
设S
△PEF=y,
∴y=

EN•PF=

×

x•(34-x)=-

x
2+

x(0<x<15);
(3)答:不可以.
证明:在折线DCB上任取一点E,连接EO并延长交AB于F.(如图3)
∵四边形ABCD是矩形,

∴AB∥CD.
∴∠ODE=∠OBF.
∵OD=OB=r,∠DOE=∠FOB,
∴△ODE≌△OBF.
∴S
△ODE=S
△OBF∴S
梯形ADEF=S
四边形ADOF+S
△ODE=S
四边形ADOF+S
△OBF=S
△ABD同理,S
梯形BCEF=S
△BCD∵S
△BCD=S
△ABD∴直线EF所割矩形PBCD面积相等.
由△ODE≌△OBF可得DE=BF.
∴DE+AD+AF=BF+AD+AF=AD+AB,

BF+BC+CE=DE+BC+CE=BC+CD.
∵AD=BC,AB=CD,
∴直线EF所割矩形PBCD周长相等.
∵这样的E点无数
而直线F″E″不能平分三角形DPA的周长和面积,
∴不存在BF(如图4).
分析:(1)由四边形是圆内接矩形可知,∠PAD=90°.根据勾股定理便可求出AD的长.
因为PD是⊙O的切线,所以根据切线的性质和直径所对的圆周角是90°构造直角三角形,应用三角函数即可求出AD与AB的长;
(2)因为PE=x,所以根据EN=PE•sin∠P=

x.建立起EN和x之间的关系,利用三角形的面积公式求出y关于x的函数关系式;
(3)过O作直线EF,利用矩形的性质,S
△ODE=S
△OBF,S
△BCD=S
△ABD,可推出直线EF所割矩形PBCD面积相等.
由△ODE≌△OBF可得DE=BF,又因为AD=BC,AB=CD,所以可计算出直线EF所割矩形ABCD周长相等.
点评:此题不仅考查了求圆的弦长等基础知识,还考查了利用面积建立函数关系式、探索与圆相关的四边形的周长和面积的等量关系等内容,有一定的开放性,旨在考查同学们的探索发现能力.

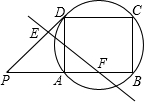 线EF能否将四边形PBCD的周长和面积同时平分?若能,请求出BF的长.若不能,请说明理由.
线EF能否将四边形PBCD的周长和面积同时平分?若能,请求出BF的长.若不能,请说明理由. 解:(1)连接BD.(如图1)
解:(1)连接BD.(如图1) =
= =
= ,
, =
= .
. =16;
=16;
 x.
x. EN•PF=
EN•PF= ×
× x•(34-x)=-
x•(34-x)=- x2+
x2+ x(0<x<15);
x(0<x<15);

 x.建立起EN和x之间的关系,利用三角形的面积公式求出y关于x的函数关系式;
x.建立起EN和x之间的关系,利用三角形的面积公式求出y关于x的函数关系式;


 34、如图:在平行四边形ABCD中,∠B=30°,AE⊥BC于点E,AF⊥DC的延长线于点F,已知平行四边形ABCD的周长为40cm,且AE:AF=2:3.求平行四边形ABCD的面积.
34、如图:在平行四边形ABCD中,∠B=30°,AE⊥BC于点E,AF⊥DC的延长线于点F,已知平行四边形ABCD的周长为40cm,且AE:AF=2:3.求平行四边形ABCD的面积. 如图,已知在四边形ABCD中,AC与BD相交于点O,AB⊥AC,CD⊥BD.
如图,已知在四边形ABCD中,AC与BD相交于点O,AB⊥AC,CD⊥BD. 如图,已知平行四边形ABCD,E是边AB的中点,联结AC、DE交于点O.记向量
如图,已知平行四边形ABCD,E是边AB的中点,联结AC、DE交于点O.记向量