
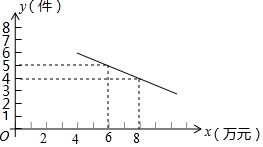
 ij��˾����ijһ������ͨѶ��Ʒ����֪ÿ����Ʒ�Ľ���Ϊ4��Ԫ��ÿ�����۸��ֲ�Ʒ���ܿ�֧���������ۣ��ܼ�11��Ԫ�������۹����з��֣���������y�����������۵���x ����Ԫ��֮���������ͼ��ʾ��һ�κ�����ϵ��
ij��˾����ijһ������ͨѶ��Ʒ����֪ÿ����Ʒ�Ľ���Ϊ4��Ԫ��ÿ�����۸��ֲ�Ʒ���ܿ�֧���������ۣ��ܼ�11��Ԫ�������۹����з��֣���������y�����������۵���x ����Ԫ��֮���������ͼ��ʾ��һ�κ�����ϵ������ ��1�����ݺ���ͼ�����ô���ϵ�������ɵã�
��2�����ݡ�������=���������������-�ܿ�֧���г���������ʽ���ɶ��κ��������ʿɵ���ֵ��
��3���ɡ����ۻ���������5��Ԫ����϶��κ�����ͼ��ó�x�ķ�Χ���ٸ��������������Ҫʹ�»���������5��Ԫ�ɵô𰸣�
��� �⣺��1����y=kx+b��
���㣨6��5������8��4�����룬�ã�
$\left\{\begin{array}{l}{6k+b=5}\\{8k+b=4}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=8}\end{array}\right.$��
��y=-$\frac{1}{2}$x+8��
��2����������ã�
z=��x-4��y-11
=��x-4����-$\frac{1}{2}$x+8��-11
=-$\frac{1}{2}$x2+10x-43
=-$\frac{1}{2}$��x-10��2+7��
�൱x=10��Ԫʱ������»���Ϊ7��Ԫ��
��3����z=5���ã�5=-$\frac{1}{2}$x2+10x-43��
�����ã�x2-20x+96=0��
��ã�x1=8��x2=12��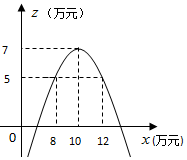
��ͼ���֪��Ҫʹ�»���������5��Ԫ�����۵���Ӧ��8��Ԫ��12��Ԫ֮�䣮
�����۵���Խ�ͣ�������Խ��
��Ҫʹ�����������Ҫʹ�»���������5��Ԫ�����۵���Ӧ��Ϊ8��Ԫ��
���� ������Ҫ������κ�����Ӧ�ã��������մ���ϵ������������ʽ�����κ�����ͼ��������ǽ���Ĺؼ���


 �߲������Ӧ��һ��ͨϵ�д�
�߲������Ӧ��һ��ͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 7m+8n=8m+7n | B�� | 7m+8n=15mn | C�� | 7m+8n=8n+7m | D�� | 7m+8n=56mn |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
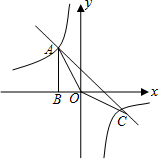 ��ͼ����A��-1��m����˫����y1=$\frac{k}{x}$��ֱ��y2=-x-��k+1���ڵڶ����Ľ��㣬��һ������C�ڵ������ޣ�AB��x����B����cos��AOB=$\frac{\sqrt{10}}{10}$
��ͼ����A��-1��m����˫����y1=$\frac{k}{x}$��ֱ��y2=-x-��k+1���ڵڶ����Ľ��㣬��һ������C�ڵ������ޣ�AB��x����B����cos��AOB=$\frac{\sqrt{10}}{10}$�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
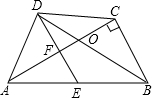 ���ı���ABCD�У�BDƽ�֡�ABC��EΪAB���е㣬DE��CB����ACB=90�㣬����Ľ����У���ȷ���Т٢ۢܣ��١�BDEΪ���������Σ��ڡ�AED=��AOD����AO•OC=DO•OB���ܡ�CAB=30��ʱ���ı���BCDEΪ���Σ�
���ı���ABCD�У�BDƽ�֡�ABC��EΪAB���е㣬DE��CB����ACB=90�㣬����Ľ����У���ȷ���Т٢ۢܣ��١�BDEΪ���������Σ��ڡ�AED=��AOD����AO•OC=DO•OB���ܡ�CAB=30��ʱ���ı���BCDEΪ���Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
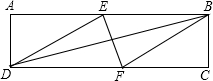 ��ͼ���ھ���ABCD�У���һ������BFDE����E��F�ֱ����߶�AB��CD�ϣ��������ǵ�����ֱ�ΪSABCD��SBFDE���ָ����������⣺
��ͼ���ھ���ABCD�У���һ������BFDE����E��F�ֱ����߶�AB��CD�ϣ��������ǵ�����ֱ�ΪSABCD��SBFDE���ָ����������⣺| A�� | ����ȷ������ȷ | B�� | ����ȷ���ڴ��� | C�� | �ٴ�����ȷ | D�� | �ٴ��ڴ��� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com