
 如图,△ABC中,AB=4,∠BAC=30°,若在AC、AB上各取一点M、N使BM+MN的值最小,则这个最小值为2$\sqrt{3}$.
如图,△ABC中,AB=4,∠BAC=30°,若在AC、AB上各取一点M、N使BM+MN的值最小,则这个最小值为2$\sqrt{3}$. 分析 作点B关于AC的对称点B,过B′作B′N⊥AB于N,交AC于M.此时BM+MN的值最小.通过证明△B′AB是等边三角形,根据等边三角形的性质求解.
解答 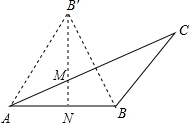 解:如图,作点B关于AC的对称点B,过B′作B′N⊥AB于N,交AC于M.此时BM+MN的值最小.
解:如图,作点B关于AC的对称点B,过B′作B′N⊥AB于N,交AC于M.此时BM+MN的值最小.
BM+MN=B′N.
∵点B′与点B关于AC对称
∴AB′=AB
又∵∠BAC=30°,
∴∠B′AB=60°,
∴△B′AB是等边三角形
∴B′B=AB=4,∠B′BN=60°,
又∵B′N⊥AB,
∴B′N=B′B=2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 本题考查的是轴对称-最短路线问题,等边三角形的判定和性质,难度较大.


科目:初中数学 来源: 题型:填空题
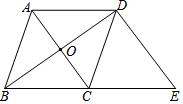 如图,在菱形ABCD中,对角线AC、BD相交于点O,且AB=5,AC=6,过点D作AC的平行线交BC的延长线于点E,则△BDE的面积为24.
如图,在菱形ABCD中,对角线AC、BD相交于点O,且AB=5,AC=6,过点D作AC的平行线交BC的延长线于点E,则△BDE的面积为24.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=$5\sqrt{5}$,则下列结论:①AC⊥BD;②AC⊥CD;③tan∠DAC=2;④四边形ABCD的面积为31;⑤BD=2$\sqrt{41}$.正确的是②③④⑤.
如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=$5\sqrt{5}$,则下列结论:①AC⊥BD;②AC⊥CD;③tan∠DAC=2;④四边形ABCD的面积为31;⑤BD=2$\sqrt{41}$.正确的是②③④⑤.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在 Rt△ABC中,∠ABC是直角,AB=4,BC=2$\sqrt{5}$,P是BC边上的动点,设BP=x,若能在AC边上找到一点Q,使∠BQP=90°,则x的取值范围是$\frac{8\sqrt{5}}{5}$≤x≤2$\sqrt{5}$.
如图,在 Rt△ABC中,∠ABC是直角,AB=4,BC=2$\sqrt{5}$,P是BC边上的动点,设BP=x,若能在AC边上找到一点Q,使∠BQP=90°,则x的取值范围是$\frac{8\sqrt{5}}{5}$≤x≤2$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,小敏站在一栋高为17米的建筑物(AC)前仰视建筑物的顶端的仰角为40°,眼睛距地面的高度(ED)为1.6米,则小敏距离建筑物的距离(DC)约为18.33米(精确到0.01).(参考数值:sin40°≈0.64,tan40°≈0.84,cos40°≈0.77)
如图,小敏站在一栋高为17米的建筑物(AC)前仰视建筑物的顶端的仰角为40°,眼睛距地面的高度(ED)为1.6米,则小敏距离建筑物的距离(DC)约为18.33米(精确到0.01).(参考数值:sin40°≈0.64,tan40°≈0.84,cos40°≈0.77)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将直角三角板60°角的顶点方在圆心O上,斜边和一直角边分别与⊙O相交于A、B两点,P是优弧AB上任意一点(与A、B不重合),则∠APB=( )
如图,将直角三角板60°角的顶点方在圆心O上,斜边和一直角边分别与⊙O相交于A、B两点,P是优弧AB上任意一点(与A、B不重合),则∠APB=( )| A. | 30° | B. | 45° | C. | 50° | D. | 60° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com