
 如图,小敏站在一栋高为17米的建筑物(AC)前仰视建筑物的顶端的仰角为40°,眼睛距地面的高度(ED)为1.6米,则小敏距离建筑物的距离(DC)约为18.33米(精确到0.01).(参考数值:sin40°≈0.64,tan40°≈0.84,cos40°≈0.77)
如图,小敏站在一栋高为17米的建筑物(AC)前仰视建筑物的顶端的仰角为40°,眼睛距地面的高度(ED)为1.6米,则小敏距离建筑物的距离(DC)约为18.33米(精确到0.01).(参考数值:sin40°≈0.64,tan40°≈0.84,cos40°≈0.77) 分析 先由AC=17,BC=ED=1.6,得出AB=AC-BC=17-1.6=15.4.再解直角△ABE,求出BE=$\frac{AB}{tan∠AEB}$≈$\frac{15.4}{0.84}$≈18.33,根据DC=BE即可求解.
解答 解:∵AC=17,BC=ED=1.6,
∴AB=AC-BC=17-1.6=15.4.
在直角△ABE中,∵∠ABE=90°,∠AEB=40°,AB=15.4,
∴BE=$\frac{AB}{tan∠AEB}$≈$\frac{15.4}{0.84}$≈18.33,
∴DC=BE≈18.33.
答:小敏距离建筑物的距离(DC)约为18.33米.
故答案为18.33米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,根据锐角三角函数的定义得出BE的长是解答此题的关键.


科目:初中数学 来源: 题型:填空题
 如图,△ABC中,AB=4,∠BAC=30°,若在AC、AB上各取一点M、N使BM+MN的值最小,则这个最小值为2$\sqrt{3}$.
如图,△ABC中,AB=4,∠BAC=30°,若在AC、AB上各取一点M、N使BM+MN的值最小,则这个最小值为2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 当n<0时,m<x1 | B. | 当n<0时,m>x2 | C. | 当n>0时,x1<m<x2 | D. | 当n>0时,m>x1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
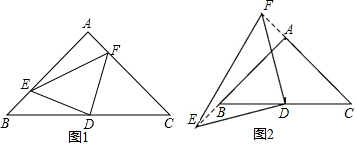
 如图,把一张三角形纸片ABC沿中位线DE剪开后,在平面上将△ADE绕着点E顺时针旋转180°,点D运动到点F的位置,则S△ADE:S四边形DBCF是1:4.
如图,把一张三角形纸片ABC沿中位线DE剪开后,在平面上将△ADE绕着点E顺时针旋转180°,点D运动到点F的位置,则S△ADE:S四边形DBCF是1:4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com