
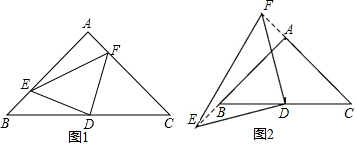
分析 (1)题要通过构建全等三角形来求解.连接AD,可通过证△ADF和△BDE全等来求本题的结论.
(2)与(1)题的思路和解法一样.
解答  (1)证明:连接AD,
(1)证明:连接AD,
∵AB=AC,∠A=90°,D为BC中点
∴AD=$\frac{BC}{2}$=BD=CD
且AD平分∠BAC
∴∠BAD=∠CAD=45°
在△BDE和△ADF中,
$\left\{\begin{array}{l}{BD=AD}\\{∠B=∠DAF=45°}\\{BE=AF}\end{array}\right.$
∴△BDE≌△ADF(SAS)
∴DE=DF,∠BDE=∠ADF
∵∠BDE+∠ADE=90°
∴∠ADF+∠ADE=90°
即:∠EDF=90°
∴△EDF为等腰直角三角形.
(2)仍为等腰直角三角形.
理由:∵△AFD≌△BED
∴DF=DE,∠ADF=∠BDE
∵∠ADF+∠FDB=90°
∴∠BDE+∠FDB=90°
即:∠EDF=90°
∴△EDF为等腰直角三角形.
点评 本题综合考查了等腰三角形的性质及判定、全等三角形的判定和性质等知识,难度较大.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,小敏站在一栋高为17米的建筑物(AC)前仰视建筑物的顶端的仰角为40°,眼睛距地面的高度(ED)为1.6米,则小敏距离建筑物的距离(DC)约为18.33米(精确到0.01).(参考数值:sin40°≈0.64,tan40°≈0.84,cos40°≈0.77)
如图,小敏站在一栋高为17米的建筑物(AC)前仰视建筑物的顶端的仰角为40°,眼睛距地面的高度(ED)为1.6米,则小敏距离建筑物的距离(DC)约为18.33米(精确到0.01).(参考数值:sin40°≈0.64,tan40°≈0.84,cos40°≈0.77)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将直角三角板60°角的顶点方在圆心O上,斜边和一直角边分别与⊙O相交于A、B两点,P是优弧AB上任意一点(与A、B不重合),则∠APB=( )
如图,将直角三角板60°角的顶点方在圆心O上,斜边和一直角边分别与⊙O相交于A、B两点,P是优弧AB上任意一点(与A、B不重合),则∠APB=( )| A. | 30° | B. | 45° | C. | 50° | D. | 60° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com