
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:填空题
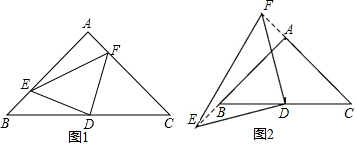
 如图,把一张三角形纸片ABC沿中位线DE剪开后,在平面上将△ADE绕着点E顺时针旋转180°,点D运动到点F的位置,则S△ADE:S四边形DBCF是1:4.
如图,把一张三角形纸片ABC沿中位线DE剪开后,在平面上将△ADE绕着点E顺时针旋转180°,点D运动到点F的位置,则S△ADE:S四边形DBCF是1:4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:①b2-4ac>0;②abc>0;③m>2.其中正确结论的个数是2个.
已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:①b2-4ac>0;②abc>0;③m>2.其中正确结论的个数是2个.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
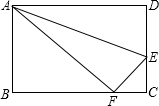 如图,在长方形ABCD(长方形四个角都是直角,并且对边相等)中,DC=5,点E在DC上,沿AE折叠△ADE,使D点与BC边上的点F重合,△ABF的面积是30,求DE的长.
如图,在长方形ABCD(长方形四个角都是直角,并且对边相等)中,DC=5,点E在DC上,沿AE折叠△ADE,使D点与BC边上的点F重合,△ABF的面积是30,求DE的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com