
分析 (1)原式利用单项式乘除单项式法则计算即可得到结果;
(2)原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分即可得到结果;
(3)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到结果,求出不等式组的整数解确定出x的值,代入计算即可求出值.
解答 解:(1)原式=-8x2y4•$\frac{3x}{4{y}^{6}}$•(-$\frac{6z}{{x}^{2}y}$)=$\frac{36xz}{{y}^{3}}$;
(2)原式=$\frac{a}{a-1}$•$\frac{(a-1)^{2}}{a}$=a-1;
(3)原式=$\frac{-{x}^{2}}{x(x+1)}$•$\frac{(x+1)^{2}}{(x+1)(x-1)}$=-$\frac{x}{x-1}$,
不等式组$\left\{\begin{array}{l}{-x≤1}\\{2x-1<4}\end{array}\right.$,
解得:-1≤x<$\frac{5}{2}$,整数解为-1,0,1,2,
当x=-1,0,1时,原式没有意义,舍去;
当x=2时,原式=-2.
点评 此题考查了分式的化简求值,一元一次不等式组的整数解,以及分式的乘除法,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:选择题
 在“两学一做”活动中,某社区居民在一幅长90cm,宽40cm的矩形形状的宣传画的四周加上宽度相同的边框,制成一幅挂图(如图),如果宣传画的面积占这个挂图面积的72%,所加边框的宽度为xcm,则根据题意列出的方程是( )
在“两学一做”活动中,某社区居民在一幅长90cm,宽40cm的矩形形状的宣传画的四周加上宽度相同的边框,制成一幅挂图(如图),如果宣传画的面积占这个挂图面积的72%,所加边框的宽度为xcm,则根据题意列出的方程是( )| A. | (90+x)(40+x)=90×40×72% | B. | (90-2x)(40-2x)=90×40×72% | ||
| C. | (90+2x)(40+2x)×72%=90×40 | D. | (90+x)(40+x)×72%=90×40 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
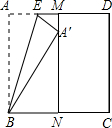 如图,正方形纸片ABCD的边长为1,M、N分别是AD、BC边上的点,且AB∥MN,将纸片的一角沿过点B的直线折叠,使A落在MN上,落点记为A′,折痕交AD于点E,若M是AD边上距D点最近的n等分点(n≥2,且n为整数),则A′N=$\frac{\sqrt{2n-1}}{n}$.
如图,正方形纸片ABCD的边长为1,M、N分别是AD、BC边上的点,且AB∥MN,将纸片的一角沿过点B的直线折叠,使A落在MN上,落点记为A′,折痕交AD于点E,若M是AD边上距D点最近的n等分点(n≥2,且n为整数),则A′N=$\frac{\sqrt{2n-1}}{n}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com