
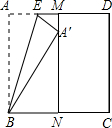
 如图,正方形纸片ABCD的边长为1,M、N分别是AD、BC边上的点,且AB∥MN,将纸片的一角沿过点B的直线折叠,使A落在MN上,落点记为A′,折痕交AD于点E,若M是AD边上距D点最近的n等分点(n≥2,且n为整数),则A′N=$\frac{\sqrt{2n-1}}{n}$.
如图,正方形纸片ABCD的边长为1,M、N分别是AD、BC边上的点,且AB∥MN,将纸片的一角沿过点B的直线折叠,使A落在MN上,落点记为A′,折痕交AD于点E,若M是AD边上距D点最近的n等分点(n≥2,且n为整数),则A′N=$\frac{\sqrt{2n-1}}{n}$. 分析 根据翻折变换的性质可得A′B=AB,再根据点M的位置求出BN,然后利用勾股定理列式计算即可得解.
解答 解:∵将纸片的一角沿过点B的直线折叠,A落在MN上,落点记为A′,
∴A′B=AB=1,
∵AB∥MN,M是AD边上距D点最近的n等分点,
∴MD=NC=$\frac{1}{n}$,
∴BN=BC-NC=1-$\frac{1}{n}$=$\frac{n-1}{n}$,
在Rt△A′BN中,根据勾股定理得,A′N2=A′B2-BN2=12-($\frac{n-1}{n}$)2=$\frac{2n-1}{{n}^{2}}$,
所以,A′N=$\sqrt{\frac{2n-1}{{n}^{2}}}$=$\frac{\sqrt{2n-1}}{n}$.
故答案为:$\frac{\sqrt{2n-1}}{n}$.
点评 本题考查了翻折变换的性质,正方形的性质,勾股定理,主要利用了翻折前后对应边相等.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a<-3 | B. | a>$\frac{1}{2}$ | C. | -$\frac{1}{2}$<a<3 | D. | -3<a<$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
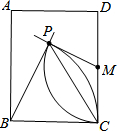 如图,长方形ABCD中,M为CD中点,分别以点B、M为圆心,以BC长、MC长为半径画弧,两弧相交于点P.若∠PMC=110°,则∠BPC的度数为( )
如图,长方形ABCD中,M为CD中点,分别以点B、M为圆心,以BC长、MC长为半径画弧,两弧相交于点P.若∠PMC=110°,则∠BPC的度数为( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平均数是30 | B. | 众数是20 | C. | 中位数是34 | D. | 方差是$\frac{176}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com