练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．已知x2+x-1=0，则代数式x3+2x2+2016=2017．

    分析 先根据已知得：x2+x=1，再将原式变形并把x2+x=1整体代入即可．

    解答 解：∵x2+x-1=0，
    ∴x2+x=1，
    ∴x3+2x2+2016，
    =x3+x2+x2+2016，
    =x（x2+x）+x2+2016，
    =x+x2+2016，
    =1+2016，
    =2017，
    故答案为：2017．

    点评 此题考查了求代数式的值及因式分解的应用，整体思想的利用是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    7．计算：$\sqrt{2}$×（-sin45°）+（π-3.14）0+（$\frac{1}{2}$）-3+|$\sqrt{3}$-tan30°|．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图，已知在Rt△ABC中，AB=AC，∠BAC=90°，AN是过点A的任一直线，BD⊥AN于点D，CE⊥AN于点E． 若BD＞CE，解答下列问题：
    （1）AD与CE的数量关系如何？请说明理由；
    （2）小贝认为DE=BD-CE，你同意她的观点吗？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．如图，在四边形ABCD中，∠ABC=90°，AB=3，BC=4，CD=10，DA=$5\sqrt{5}$，则下列结论：①AC⊥BD；②AC⊥CD；③tan∠DAC=2；④四边形ABCD的面积为31；⑤BD=2$\sqrt{41}$．正确的是②③④⑤．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．在数轴上到原点的距离为$\sqrt{3}$的点表示的数是±$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．如图，小敏站在一栋高为17米的建筑物（AC）前仰视建筑物的顶端的仰角为40°，眼睛距地面的高度（ED）为1.6米，则小敏距离建筑物的距离（DC）约为18.33米（精确到0.01）．（参考数值：sin40°≈0.64，tan40°≈0.84，cos40°≈0.77）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

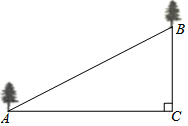    9．如图，在山坡AB上种树，已知∠C=90°，∠A=29°，相邻两树的坡面距离AB=11米，则相邻两树的水平距离AC≈9.6米．（精确到0.1米）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．计算（$\frac{1}{2}$）-1-4sin45°-（1-$\sqrt{2}$）0+$\sqrt{8}$的结果是1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．若$\frac{2}{3}x=\frac{1}{2}y$，则x：y=3：4．

    查看答案和解析>>

    同步练习册答案