
 如图所示,在正方形ABCD中,M为AB的中点,N为AD上的一点,且AN=$\frac{1}{4}$AD,试猜测△CMN是什么三角形,请证明你的结论.(提示:正方形的四条边都相等,四个角都是直角)
如图所示,在正方形ABCD中,M为AB的中点,N为AD上的一点,且AN=$\frac{1}{4}$AD,试猜测△CMN是什么三角形,请证明你的结论.(提示:正方形的四条边都相等,四个角都是直角) 分析 可设正方形ABCD的边长为4a,利用勾股定理分别求出NC,MN,CM的值,计算得出MN2+MC2=NC2,根据勾股定理的逆定理可判定△CMN是直角三角形.
解答 解:△CMN是直角三角形.理由如下:
设正方形ABCD的边长为4a,则AB=BC=CD=AD=4a.
∵M是AB的中点,
∴AM=BM=2a.
∵AN=$\frac{1}{4}$AD,AD=4a,
∴AN=a,DN=3a.
∵在Rt△AMN中,满足AM2+AN2=MN2,且AM=2a,AN=a,
∴MN=$\sqrt{5}$a.
同理可得:MC=$\sqrt{20}$a,NC=5a.
∵MN2+MC2=($\sqrt{5}$a)2+($\sqrt{20}$a)2=25a2,NC2=(5a)2=25a2,
∴MN2+MC2=NC2,
∴△CMN是直角三角形.
点评 本题考查的是勾股定理及其逆定理,正方形的性质,设正方形ABCD的边长为4a,通过计算得出MN2+MC2=NC2,是解题的关键.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:填空题
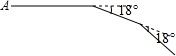 如图,小亮从A点出发前进10m,向右转18°,再前进10m,又向右转18°,…,这样一直走下去,他第一次回到出发点A时,一共走了200m.
如图,小亮从A点出发前进10m,向右转18°,再前进10m,又向右转18°,…,这样一直走下去,他第一次回到出发点A时,一共走了200m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “a不是负数”表示为a>0 | |
| B. | “m与4的差是非负数”表示为m-4≥0 | |
| C. | “x不大于3”表示为x≤3 | |
| D. | “代数式x2+3大于3x-7”表示为x2+3>3x-7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com