
【题目】如图,AD是∠BAC平分线,点E在AB上,且AE=AC,EF∥BC交AC于点F,AD与CE交于点G,与EF交于点H.
(1)证明:AD垂直平分CE;
(2)若∠BCE=40°,求∠EHD的度数.
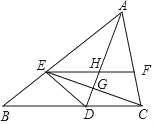
【答案】(1)见解析;(2)50°.
【解析】
(1)根据等腰三角形三线合一的性质可得出结论;(2)由(1)可知点D为CE垂直平分线上的点,则CD=DE,∠DCE=∠DEC.由EF∥BC,可得EG平分∠DEF;由EG⊥AD,可证∠EDH=∠EHD,根据内角和定理,即可得出结论.
解:(1)∵AE=AC,AD是∠BAC平分线,
∴AD垂直平分CE;
(2)由(1)可知点D为CE垂直平分线上的点,
∴CD=DE,
∴∠DCE=∠DEC.
∵EF∥BC,
∴∠DCE=∠CEF=∠DEC,
∴EG平分∠DEF.
∵EG⊥AD,EG=EG,
∴△DEG≌△HEG(ASA),
∴△DEH是等腰三角形,且ED=EH,
∴∠EDH=∠EHD,
∵∠BCE=40°,
∴∠DEH=2∠BCE=80°,
∴∠EHD=![]() (180°﹣80°)=50°.
(180°﹣80°)=50°.


科目:初中数学 来源: 题型:
【题目】如图①、②、③,正三角形ABC、正方形ABCD、正五边形ABCDE分别是⊙O的内接三角形、内接四边形、内接五边形,点M、N分别从点B,C开始,以相同的速度中⊙O上逆时针运动.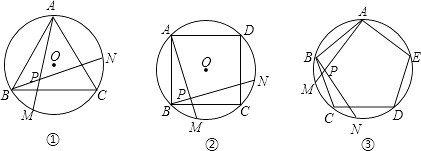
(1)求图①中∠APB的度数;
(2)图②中,∠APB的度数是 , 图③中∠APB的度数是;
(3)根据前面探索,你能否将本题推广到一般的正n边形情况?若能,写出推广问题和结论;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图: 下面是一道证明题,刘老师给同学们讲解了思路,请将证明过程和每一步的理由补充完整.
已知:∠A=∠E,AD∥BE,求证:∠1=∠2
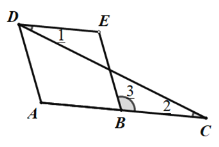
证明:![]() AD∥BE(已知)
AD∥BE(已知)
∠A= ( )
![]() ∠A=∠E ( 已知 )
∠A=∠E ( 已知 )
![]() ∠E= (等量代换)
∠E= (等量代换)
![]() DE∥AC( )
DE∥AC( )
![]() ∠1=∠2( )
∠1=∠2( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[感知发现]:如图,是一个“猪手”图,AB∥CD,点E在两平行线之间,连接BE,DE ,我们发现:∠E=∠B+∠D
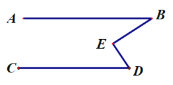
证明如下:过E点作EF∥AB.
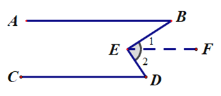
![]() ∠B=∠1(两直线平行,内错角相等.)
∠B=∠1(两直线平行,内错角相等.)
又![]() AB∥CD(已知)
AB∥CD(已知)
![]() CD∥EF(如果两条直线都与第三条直线平行,那么这两条直线也互相平行.)
CD∥EF(如果两条直线都与第三条直线平行,那么这两条直线也互相平行.)
![]() ∠2=∠D(两直线平行,内错角相等.)
∠2=∠D(两直线平行,内错角相等.)
![]() ∠1+∠2=∠B+∠D(等式的性质1.)
∠1+∠2=∠B+∠D(等式的性质1.)
即:∠E=∠B+∠D
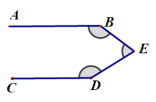
[类比探究]:如图是一个“子弹头”图,AB∥CD,点E在两平行线之间,连接BE,DE.试探究∠E+∠B+∠D=360°.写出证明过程.
[创新应用]:
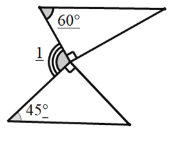
(1).如图一,是两块三角板按如图所示的方式摆放,使直角顶点重合,斜边平行,请直接写出∠1的度数.
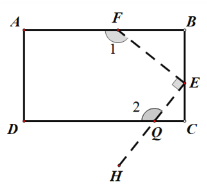
(2).如图二,将一个长方形ABCD按如图的虚线剪下,使∠1=120![]() ,∠FEQ=90°. 请直接写出∠2的度数.
,∠FEQ=90°. 请直接写出∠2的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某开发区有一块四边形的空地![]() ,如图所示,现计划在空地上种植草皮,经测量
,如图所示,现计划在空地上种植草皮,经测量![]() ,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问要多少投入?
,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问要多少投入?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道对于一个图形,通过不同的方法计算图形的面积可以得到一个数学等式.例如:由图1可得到![]() .
.

(1)写出由图2所表示的数学等式:________.

(2)写出由图3所表示的数学等式:________.

(3)已知实数![]() ,
,![]() ,
,![]() 满足
满足![]() ,
,![]() .
.
①求![]() 的值.
的值.
②求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图1是AD∥BC的一张纸条,按图1→图2→图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=18°,则图2中∠AEF的度数为( )
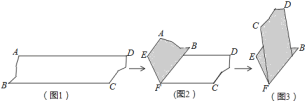
A.120°B.108°C.126°D.114°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象过(﹣2,0),则下列结论:①bc>0;②b+2a=0;③a+c>b;④16a+4b+c=0;⑤3a+c<0,其中正确结论的个数是( )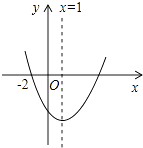
A.5
B.4
C.3
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=9,AD=6,∠ADC的平分线交AB于点E,交CB的延长线于点F,AG⊥DE,垂足为G.若AG=4 ![]() ,则△BEF的面积是( )
,则△BEF的面积是( )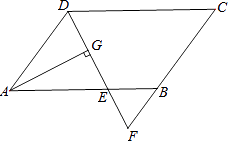
A.![]()
B.2 ![]()
C.3 ![]()
D.4 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com