分析:(1)存在P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,设BP=x,根据∠B=∠D=90°和相似三角形的判定得出当
=
或
=
时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,代入求出即可;
(2)存在P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,设BP=x,根据∠B=∠D=90°和相似三角形的判定得出当
=
或
=
时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,代入求出即可;
(3)存在P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,设BP=x,根据∠B=∠D=90°和相似三角形的判定得出当
=
或
=
时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,代入后根据根的判别式进行判断即可.
解答:解:(1)存在P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,
理由是:设BP=x,
∵AB⊥BD,CD⊥BD,
∴∠B=∠D=90°,
∴当
=
或
=
时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,
∴①
=
或②
=
,
解方程①得:x=
,经检验x=
是方程①的解,且符合题意.
方程②得:x(10-x)=36,
x
2-10x+36=0,
△=(-10)
2-4×1×36<0,此方程无解,
∴当BP=
时,以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,
∴存在P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,此时BP的值为
;
(2)在BD上存在3个P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,
理由是:设BP=x,
∵AB⊥BD,CD⊥BD,
∴∠B=∠D=90°,
∴当
=
或
=
时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,
∴①
=
或②
=
,
解方程①得:x=
,经检验x=
是方程①的解,且符合题意.
方程②得:x(15-x)=36,
x
2-15x+36=0,
△=(-15)
2-4×1×36=81,
此方程的解为x
2=3,x
3=12,经检验x
2=3,x
3=12是方程②的解,且符合题意.
∴当BP=
或3或12时,以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,
∴存在3个点P,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,此时BP的值为
或3或12;
(3)设BP=x,
∵AB⊥BD,CD⊥BD,
∴∠B=∠D=90°,
∴当
=
或
=
时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,
∴①
=
或②
=
,
解方程①得:x=
,
方程②得:x(l-x)=mn,
x
2-lx+mn=0,
△=(-l)
2-4×1×mn=l
2-4mn,
∴当l
2-4mn<0时,方程②没有实数根,
即当l
2-4mn<0时,存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的一个P点;
∵当l
2-4mn=0时,方程②有1个实数根,
∴当l
2-4mn=0时,存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的两个P点;
∵当l
2-4mn>0时,方程②有2个实数根,
∴当l
2-4mn>0时,存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的三个P点.

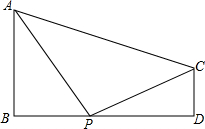 如图,已知AB⊥BD,CD⊥BD.
如图,已知AB⊥BD,CD⊥BD.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案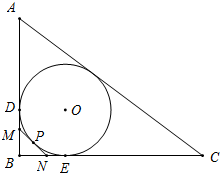 如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D、E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若AB=6cm,BC=8cm,则Rt△MBN的周长为
如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D、E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若AB=6cm,BC=8cm,则Rt△MBN的周长为