
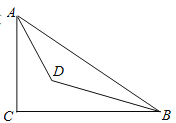
【题目】如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD和BD分别是∠BAC和∠ABC的平分线,它们相交于点D,则点D到BC的距离是______.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某校八年级两个班,各选派10名学生参加学校举行的“美丽绍兴乡土风情知识”大赛预赛各参赛选手的成绩如下:
八(1)班:88,91,92,93,93,93,94,98,98,100;
八(2)班:89,93,93,93,95,96,96,98,98,99.
通过整理,得到数据分析表如下:
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
八(1)班 | 100 | m | 93 | 93 | 12 |
八(2)班 | 99 | 95 | n | 93 | 8.4 |
(1)求表中m、n的值;
(2)依据数据分析表,有同学说:“最高分在(1)班,(1)班的成绩比(2)班好”,但也有同学说(2)班的成绩更好请您写出两条支持八(2)班成绩好的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市长途客运站每天6:30—7:30开往某县的三辆班车票价相同,但车的舒适程度不同.小张和小王因事需在这一时段乘车去该县,但不知道三辆车开来的顺序,两人采用不同的乘车方案:小张无论如何决定乘坐开来的第一辆车,而小王则是先观察后上车,当第一辆车开来时,他不上车,而是仔细观察车的舒适状况.若第二辆车的状况比第一辆车好,他就上第二辆车;若第二辆车不如第一辆车,他就上第三辆车.若按这三辆车的舒适程度分为优、中、差三等,请你思考并回答下列问题:
(1)三辆车按出现的先后顺序共有哪几种可能?
(2)请列表分析哪种方案乘坐优等车的可能性大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙P的圆心是(3,a)(a>3),⊙P与y轴相切,函数y=x的图象被⊙P截得的弦AB的长为2![]() ,则a的值是_____.
,则a的值是_____.
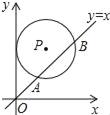
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知开口向下的抛物线y=ax2-2ax+2与y轴的交点为A,顶点为B,对称轴与x轴的交点为C,点A与点D关于对称轴对称,直线BD与x轴交于点M,直线AB与直线OD交于点N.
(1)求点D的坐标.
(2)求点M的坐标(用含a的代数式表示).
(3)当点N在第一象限,且∠OMB=∠ONA时,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
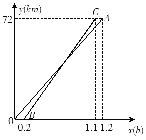
【题目】甲、乙两人周末从同一地点出发去某景点,因乙临时有事,甲先出发,甲出发0.2小时后乙开汽车前往,设甲行驶的时间为x(h),甲、乙两人行驶的路程分别为y1(km)与y2(km),如图是y1与y2关于x的函数图像.
(1)求x为何值时,两人相遇?
(2)求x为何值时,两人相距5km?(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(8,0),O为坐标原点,P是线段OA上任意一点(不含端点O、A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=5时,这两个二次函数的最大值之和等于_______
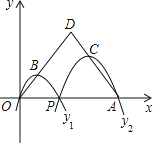
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位射击运动员参加射击训练,各射击20次,成绩如下表所示:
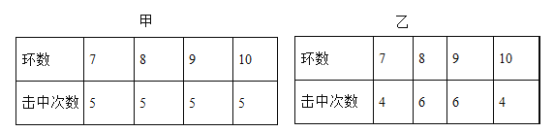
设甲、乙两位运动员射击成绩的方差分别为S 2甲和S 2乙,则下列说法正确的是
A. S 2甲<S 2乙B. S 2甲=S 2乙
C. S 2甲>S 2乙D. 无法比较S 2甲和S 2乙的大小
查看答案和解析>>
科目:初中数学 来源: 题型:
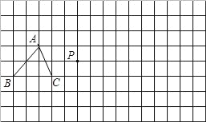
【题目】在下面16×8的正方形网格中,每个小正方形的边长为1个单位,△ABC是格点三角形(顶点在网格交点处),请你画出:
(1)△ABC关于点P的位似△A′B′C′,且位似比为1:2;
(2)以A.B.C.D为顶点的所有格点平行四边形ABCD的顶点D
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com