
【题目】如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为( )
A.17
B.18
C.19
D.20
【答案】D
【解析】解:∵O是矩形ABCD的对角线AC的中点,M是AD的中点,
∴∠ABC=∠D=90°,CD=AB=5,BC=AD=12,OA=OB,OM为△ACD的中位线,
∴OM=![]() CD=2.5,AC=
CD=2.5,AC=![]() =13,
=13,
∵O是矩形ABCD的对角线AC的中点,
∴BO=![]() AC=6.5,
AC=6.5,
∴四边形ABOM的周长为AB+AM+BO+OM=5+6+6.5+2.5=20,
故选:D.
根据题意可知OM是△ADC的中位线,得出OM![]() CD;根据勾股定理可求出AC的长,利用直角三角形斜边上的中线等于斜边的一半求出BO,进而求出四边形ABOM的周长.
CD;根据勾股定理可求出AC的长,利用直角三角形斜边上的中线等于斜边的一半求出BO,进而求出四边形ABOM的周长.
【考点精析】关于本题考查的三角形中位线定理和矩形的性质,需要了解连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;矩形的四个角都是直角,矩形的对角线相等才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】观察下来等式:
第一层 1+2=3
第二层 4+5+6=7+8
第三层 9+10+11+12=13+14+15
第四层 16+17+18+19+20=21+22+23+24
…
在上述数字宝塔中,从上往下数,数字2016在第层.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F是四边形ABCD的对角线AC上两点,AE=CF,DF∥BE,DF=BE.
(1)求证:四边形ABCD是平行四边形;
(2)若AC平分∠BAD,求证:ABCD为菱形.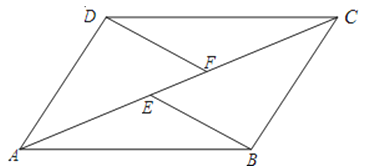
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
第一个等式: ![]()
第二个等式: ![]()
第三个等式: ![]()
第四个等式: ![]()
则式子![]() __________________;
__________________;
用含n的代数式表示第n个等式: ![]() ____________________________;
____________________________;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“滴滴快车”是一种便捷的出行工具,计价规则如下表:
计费项目 | 里程费 | 时长费 |
单价 | 1.4元/千米 | 0.5元/分钟 |
注:车费由里程费、时长费两部分构成,其中里程费按行车的实际里程计费,时长费按行车的实际时间计算。车费不足8元的按最低消费8元收取。为了推广和扩大“滴滴快车”的市场占有率,公司近期推出优惠政策,凡车费满10元,将给予8折优惠。 | ||
随着互联网的不断发展,更多的人们选择了“滴滴快车”出行。假设“滴滴快车”的平均行车速度为50 km/h,请回答下列问题:
(1)小明和小冰各自乘坐“滴滴快车”,行车里程分别为3千米和10千米,请问他们各自需付车费多少钱?
(2)张老师与王老师的家和学校在同一条直线上,位置如图所示.一天,张老师和王老师各自从学校“滴滴快车”回家,分别付车费9.6元和24元.请问,张老师和王老师的家相距多少千米?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线AB,CD相交于点O,作∠DOE=∠BOD,OF平分∠AOE.
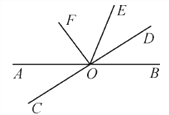
(1)判断OF与OD的位置关系;
(2)若∠AOC∶∠AOD=1∶5,求∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分解因式x2﹣m2+4mn﹣4n2等于( )
A.(x+m+2n)(x﹣m+2n)
B.(x+m﹣2n)(x﹣m+2n)
C.(x﹣m﹣2n)(x﹣m+2n)
D.(x+m+2n)(x+m﹣2n)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,D为圆周上任一点,C是弧BD的中点,CE⊥AB,垂足为E,BD交CE于点F.
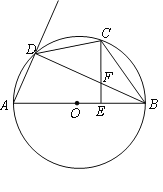
(1)求证:![]() ;
;
(2)若![]() ,⊙O的半径为3,求BC的长.
,⊙O的半径为3,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com