
【题目】如图,E、F是四边形ABCD的对角线AC上两点,AE=CF,DF∥BE,DF=BE.
(1)求证:四边形ABCD是平行四边形;
(2)若AC平分∠BAD,求证:ABCD为菱形.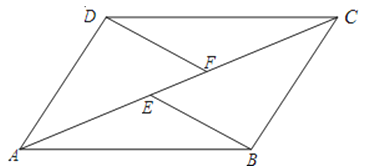
【答案】证明:(1)∵DF∥BE,
∴∠DFA=∠CEB,
∵AE=CF,
∴AE+EF=CF+EF,
即AF=CE,
在△ADF和△CBE中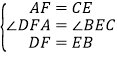 ,
,
∴△ADF≌△CBE(SAS),
∴AD=CB,∠DAC=∠ACB,
∴AD∥CB,
∴四边形ABCD是平行四边形;
(2)∵AC平分∠BAD,
∴∠DAC=∠BAC,
∴∠BAC=∠ACB,
∴AB=BC,
∴ABCD为菱形.
【解析】(1)首先证明△ADF≌△CBE,根据全等三角形的性质可得AD=CB,∠DAC=∠ACB,进而可得证明AD∥CB,根据一组对边平行且等的四边形是平行四边形可得四边形ABCD是平行四边形;
(2)首先根据角平分线的性质可得∠DAC=∠BAC,进而可得出AB=BC,再根据一组邻边相等的平行四边形是菱形可得结论.
【考点精析】认真审题,首先需要了解菱形的判定方法(任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形).


科目:初中数学 来源: 题型:
【题目】如图,P为正方形ABCD对角线AC上一动点,EF⊥AC且交AD于E,交CD的延长线于点G,连接CE和AG.
(1)求证:△ADG≌△CDE;
(2)当CE平分∠ACD时,求tan∠AGD.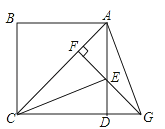
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点,DE、BF相交于点G,连接BD、CG.给出以下结论,其中正确的有( )
①∠BGD=120°;②BG+DG=CG;③△BDF≌△CGB;④S△ADE=![]() AB2 .
AB2 . 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=a,AD=b,E,F分别是AB,CD的中点,M是BC上一动点,AM,DM分别交EF于点G,H,连接CH.
(1)试判断GH是否为定值,并证明你的结论;
(2)当点M为BC的中点时,求证:四边形GMCH是平行四边形;
(3)试探究:在(2)的条件下,当a,b满足什么数量关系时,四边形GMCH是菱形?(不必证明,直接写出结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为( )
A.17
B.18
C.19
D.20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com