
【题目】如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1 , 再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2 , 如此进行下去,得到四边形AnBnCnDn . 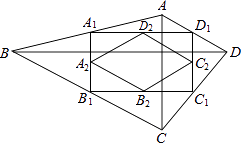
(1)求证:四边形A1B1C1D1是矩形;
(2)四边形A3B3C3D3是形;
(3)四边形A1B1C1D1的周长为;
(4)四边形AnBnCnDn的面积为 .
【答案】
(1)证明:∵在四边形ABCD中,顺次连接四边形ABCD 各边中点,得到四边形A1B1C1D1,
∴A1D1∥BD,B1C1∥BD,C1D1∥AC,A1B1∥AC;
∴A1D1∥B1C1,A1B1∥C1D1,
∴四边形A1B1C1D1是平行四边形;
∵AC丄BD,
∴四边形A1B1C1D1是矩形
(2)矩
(3)a+b
(4)![]()
【解析】(2)解:∵四边形A1B1C1D1是矩形, ∴B1D1=A1C1(矩形的两条对角线相等);
∴A2D2=C2D2=C2B2=B2A2(中位线定理),
∴四边形A2B2C2D2是菱形;
∴四边形A3B3C3D3是矩形,
所以答案是:矩; (3)解:根据三角形中位线定理可得D1C1=A1B1= ![]() AC=
AC= ![]() a,A1D1=B1C1=
a,A1D1=B1C1= ![]() BC=
BC= ![]() b.故四边形A1B1C1D1是的周长为a+b,
b.故四边形A1B1C1D1是的周长为a+b,
所以答案是:a+b.(4)解:∵四边形ABCD中,AC=a,BD=b,且AC丄BD,
∴S四边形ABCD=ab÷2;
由三角形的中位线的性质可以推知,每得到一次四边形,它的面积变为原来的一半,
四边形AnBnCnDn的面积是 ![]() .
.
所以答案是: ![]() .
.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
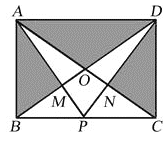
【题目】在矩形ABCD中,AB=6,BC=8,AC,BD相交于O,P是边BC上一点,AP与BD交于点M,DP与AC交于点N.
①若点P为BC的中点,则AM:PM=2:1;
②若点P为BC的中点,则四边形OMPN的面积是8;
③若点P为BC的中点,则图中阴影部分的总面积为28;
④若点P在BC的运动,则图中阴影部分的总面积不变.
其中正确的是_____________.(填序号即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
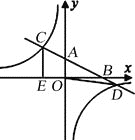
【题目】如图,在平面直角坐标系xOy中,直线y=﹣![]() x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2.
x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2.
(1)求反比例函数的解析式;
(2)连接OD,求△OBD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=AB·AD,我们称该四边形为“可分四边形”,∠DAB称为“可分角”.
(1)如图2,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB,则∠DAB=_________.
(2)如图3,在四边形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求证:四边形ABCD为“可分四边形”;
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,BC=2,∠D=90°,求AD的长?

图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的面积为16cm2 , 对交线交于点O;以AB、AO为邻边作平行四边AOC1B,对角线交于点O1 , 以AB、AO1为邻边作平行四边形AO1C2B,…;依此类推,则平行四边形AO4C5B的面积为( ) 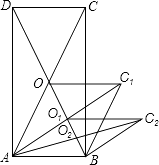
A.![]() cm2
cm2
B.1cm2
C.2cm2
D.4cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工艺商场按标价销售某种工艺品时,每件可获利45元;按标价的八五折销售该工艺品8件与将标价降低35元销售该工艺品12件所获利润相等.
(1)该工艺品每件的进价、标价分别是多少元?
(2)若每件工艺品按(1)中求得的进价进货,标价售出,工艺商场每天可售出该工艺品100件.若每件工艺品降价1元,则每天可多售出该工艺品4件.问每件工艺品降价多少元出售,每天获得的利润最大?获得的最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com