
【题目】如图,在△ABC中,AB=AC,PE⊥AB,PF⊥AC,CD⊥AB,垂足分别为E、D、F,求证:PE﹣PF=CD. 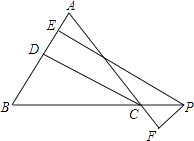
【答案】证明:过C作CG⊥PE于G, ∵PE⊥AB,CD⊥AB,CG⊥PE,
∴四边形CDEG是矩形,
∴CD=EG,
∵PF⊥AC,
∴∠PFC=90°,
∵CG⊥PE,
∴∠PGC=90°,
∴∠PFC=∠PGC,
∵AB=AC,
∴∠ABC=∠ACB,
∵CG⊥PE,AB⊥PE,
∴CG∥AB,
∴∠ABC=∠PCG,
又∵∠ACB=∠PCF(对顶角相等),
∴∠PCG=∠PCF,
在△PCG和△PCF中,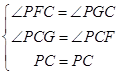 ,
,
∴△PCG≌△PCF(AAS),
∴PF=PG,
∴PE﹣PG=PE﹣PF=EG=CD,
则PE﹣PF=CD.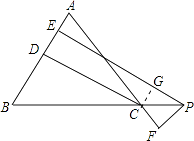
【解析】过C作CG⊥PE于G,由三个角为直角的四边形为矩形得到CDEG为矩形,得到CD=EG,由一对直角相等,一对对顶角相等,且AC=AC,利用AAS得到三角形PCG与三角形PCF全等,利用全等三角形边相等得到PF=PG,由PE﹣PG=PE﹣PF=EG=CD,即可得证.
【考点精析】本题主要考查了等腰三角形的性质的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角)才能正确解答此题.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1 , 再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2 , 如此进行下去,得到四边形AnBnCnDn . 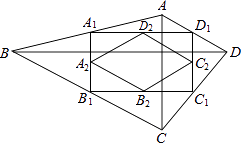
(1)求证:四边形A1B1C1D1是矩形;
(2)四边形A3B3C3D3是形;
(3)四边形A1B1C1D1的周长为;
(4)四边形AnBnCnDn的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
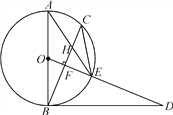
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
求证:(1)BD是⊙O的切线;
(2)若EH=2,AH=6,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知圆的半径为r,圆心到直线a的距离为d,d和r分别是方程x2﹣7x+10=0的两根,则直线a与圆的位置关系是( )
A. 相交B. 相切C. 相交或相离D. 相离
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题。
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:CN∥AB.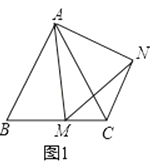
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论CN∥AB还成立吗?请说明理由.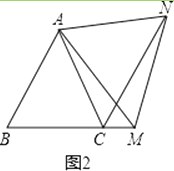
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要使式子-7ab-14abx+49aby=-7ab( )的左边与右边相等,则“( )”内应填的式子是( )
A. -1+2x+7y B. -1-2x+7y
C. 1-2x-7y D. 1+2x-7y
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中任意一点P(x0 , y0),经平移后对应点为P1(x0+3,y0﹣3),将△ABC作同样平移得到△DEF. 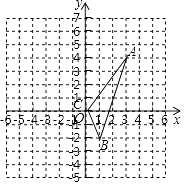
(1)求△ABC的面积;
(2)请写出D,E,F的坐标,并在图中画出△DEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京沈高铁赤峰至喀左段于2016年开工建设,天义镇路基桥墩建设初具规模,预计2019年运营,从赤峰出发经宁城至北京500公里,高铁运行速度将是现行普通客车平均速度的5倍,预计开通后,从赤峰出发,某高铁客运专列比普通客车晚3小时开出,但比普通客车早5小时到达北京,求两车的运行速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com