
【题目】如图,已知在△ABC中任意一点P(x0 , y0),经平移后对应点为P1(x0+3,y0﹣3),将△ABC作同样平移得到△DEF. 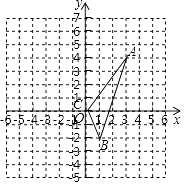
(1)求△ABC的面积;
(2)请写出D,E,F的坐标,并在图中画出△DEF.
 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】工艺商场按标价销售某种工艺品时,每件可获利45元;按标价的八五折销售该工艺品8件与将标价降低35元销售该工艺品12件所获利润相等.
(1)该工艺品每件的进价、标价分别是多少元?
(2)若每件工艺品按(1)中求得的进价进货,标价售出,工艺商场每天可售出该工艺品100件.若每件工艺品降价1元,则每天可多售出该工艺品4件.问每件工艺品降价多少元出售,每天获得的利润最大?获得的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△A′ B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3,若∠B+∠B′=90°,则△ABC与△A′B′C′的面积比为 _______。
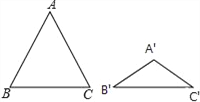
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据已知条件写出相应不等式.
(1)-3,-2,-1,0,1都是不等式的解;
(2)不等式的负整数解只有-1,-2,-3;
(3)不等式的解的最大的值是0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD,BD分别平分∠CAB和∠CBA,相交于点D. 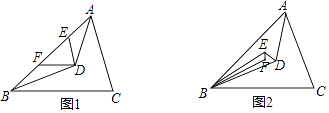
(1)如图1,过点D作DE∥AC,DF∥BC分别交AB于点E、F. ①若∠EDF=80°,则∠C为多少?
②若∠EDF=x°,证明:∠ADB=(90+ ![]() )°.
)°.
(2)如图2,若DE,BE分别平分∠ADB和∠ABD,且EF,BF分别平分∠BED和∠EBD,若∠BFE的度数是整数,求∠BFE至少是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列式子中去括号错误的是( )
A.5x﹣(x﹣2y)=5x﹣x+2y
B.2a2+(3a﹣b)=2a2+3a﹣b
C.(x﹣2y)﹣(x2﹣y2)=x﹣2y﹣x2+y2
D.3x2﹣3(x+6)=3x2﹣3x﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是按规律摆放在墙角的一些小正方体,从上往下分别记为第一层,第二层,第三层…第n层… 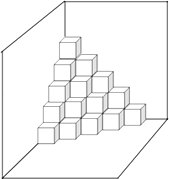
(1)第三层有个小正方体.
(2)从第四层至第六层(含第四层和第六层)共有个小正方体.
(3)第n层有个小正方体.
(4)若每个小正方体边长为a分米,共摆放了n层,则要将摆放的小正方体能看到的表面部分涂上防锈漆,则防锈漆的总面积为分米2 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com