
【题目】如图,在△ABC中,AD,BD分别平分∠CAB和∠CBA,相交于点D. 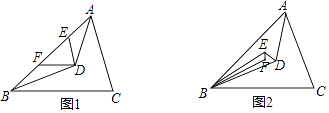
(1)如图1,过点D作DE∥AC,DF∥BC分别交AB于点E、F. ①若∠EDF=80°,则∠C为多少?
②若∠EDF=x°,证明:∠ADB=(90+ ![]() )°.
)°.
(2)如图2,若DE,BE分别平分∠ADB和∠ABD,且EF,BF分别平分∠BED和∠EBD,若∠BFE的度数是整数,求∠BFE至少是多少度?
【答案】
(1)解:∵∠EDF=80°,
∴∠DEF+∠EDF=180°﹣80°=100°,
∵DE∥AC,
∴∠BED=∠BAC,
同理得:∠EFD=∠ABC,
∴∠ABC+∠BAC=∠DEF+∠EDF=100°,
∴∠C=80°
故答案为:80°;
②∵∠EDF=x°,
∴∠DEF+∠EFD=180°﹣x°,
∵DE∥AC,
∴∠BED=∠BAC,
∵AD平分∠BAC,
∴∠BAC=2∠BAD,
∴∠DEF=2∠BAD,
同理得:∠EFD=2∠ABD,
∴∠BAD+∠ABD= ![]() ,
,
∴∠ADB=180°﹣∠ABD﹣∠BAD=180°﹣ ![]() =90°+
=90°+ ![]() =(90+
=(90+ ![]() )°
)°
(2)解:∵DE平分∠ADB,
∴∠BDE= ![]() ∠ADB=45°+
∠ADB=45°+ ![]() ,
,
∵∠BED+∠DBE=180°﹣∠BDE,
∵EF,BF分别平分∠BED和∠EBD,
∴ ![]() ∠BED+
∠BED+ ![]() ∠DBE=90°﹣
∠DBE=90°﹣ ![]() ∠BDE,
∠BDE,
即∠BEF+∠EBF=90°﹣ ![]() ∠BDE,
∠BDE,
∴∠BFE=180°﹣(∠BEF+∠EBF),
=180°﹣(90°﹣ ![]() ∠BDE),
∠BDE),
=90°+ ![]() ∠BDE,
∠BDE,
=90°+ ![]() (45°+
(45°+ ![]() ),
),
=90°+22°+ ![]() +
+ ![]() ,
,
=112°+ ![]() ,
,
∵∠BFE的度数是整数,
当x=4时,∠BFE=113°.
答:∠BFE至少是113度
【解析】(1)①先根据三角形的内角和求得:∠DEF+∠EDF=100°,再由平行线的性质得:∠BED=∠BAC,∠EFD=∠ABC,所以∠C=180°﹣100°=80°;②同理先求出∠DEF+∠EFD=180°﹣x°,由平行线的性质和角平分线的定义得:∠DEF=2∠BAD,同理得:∠EFD=2∠ABD,则∠BAD+∠ABD= ![]() ,再由三角形内角和可求得结论;(2)依据②的结论得:∠ADB=(90+
,再由三角形内角和可求得结论;(2)依据②的结论得:∠ADB=(90+ ![]() )°,则∠BDE=
)°,则∠BDE= ![]() ∠ADB=45°+
∠ADB=45°+ ![]() ,由三角形的内角和定理得:∠BED+∠DBE=180°﹣∠BDE,再由角平分线定义得:
,由三角形的内角和定理得:∠BED+∠DBE=180°﹣∠BDE,再由角平分线定义得: ![]() ∠BED+
∠BED+ ![]() ∠DBE=90°﹣
∠DBE=90°﹣ ![]() ∠BDE,代入∠BFE=180°﹣(∠BEF+∠EBF),可得结论.
∠BDE,代入∠BFE=180°﹣(∠BEF+∠EBF),可得结论.
【考点精析】本题主要考查了平行线的性质和三角形的内角和外角的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】综合题。
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:CN∥AB.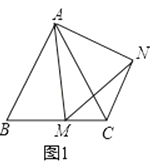
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论CN∥AB还成立吗?请说明理由.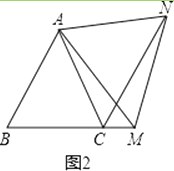
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:

组号 | 分组 | 频数 |
一 | 6≤m<7 | 2 |
二 | 7≤m<8 | 7 |
三 | 8≤m<9 | a |
四 | 9≤m≤10 | 2 |
(1)求a的值.
(2)若用扇形统计图来描述,求分数在8≤m<9内所对应的扇形的圆心角的度数.
(3)将在第一组内的两名选手记为A1,A2,在第四组内的两名选手记为B1,B2, 从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中任意一点P(x0 , y0),经平移后对应点为P1(x0+3,y0﹣3),将△ABC作同样平移得到△DEF. 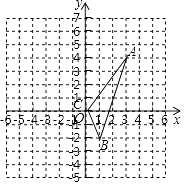
(1)求△ABC的面积;
(2)请写出D,E,F的坐标,并在图中画出△DEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
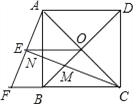
【题目】如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.
(1)已知BD=![]() ,求正方形ABCD的边长;
,求正方形ABCD的边长;
(2)猜想线段EM与CN的数量关系并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l外不重合的两点A、B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:①作点B关于直线l的对称点B′;②连接AB′与直线l相交于点C,则点C为所求作的点.在解决这个问题时没有运用到的知识或方法是( )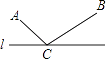
A.转化思想
B.三角形的两边之和大于第三边
C.两点之间,线段最短
D.三角形的一个外角大于与它不相邻的任意一个内角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为______

查看答案和解析>>
科目:初中数学 来源: 题型:
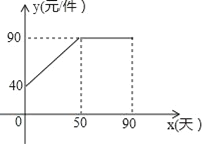
【题目】九年级某班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
时间x(天) | 1 | 30 | 60 | 90 |
每天销售量p(件) | 198 | 140 | 80 | 20 |
(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com