
【题目】如图,直线l外不重合的两点A、B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:①作点B关于直线l的对称点B′;②连接AB′与直线l相交于点C,则点C为所求作的点.在解决这个问题时没有运用到的知识或方法是( )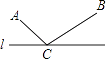
A.转化思想
B.三角形的两边之和大于第三边
C.两点之间,线段最短
D.三角形的一个外角大于与它不相邻的任意一个内角
科目:初中数学 来源: 题型:
【题目】某服装店以每件82元的价格购进了30套保暖内衣,销售时,针对不同的顾客,这30套保暖内衣的售价不完全相同,若以100元为标准,将超过的钱数记为正,不足的钱数记为负,则记录结果如表所示:
售出件数 | 7 | 6 | 7 | 8 | 2 |
售价(元) | +5 | +1 | 0 | ﹣2 | ﹣5 |
请你求出该服装店在售完这30套保暖内衣后,共赚了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△A′ B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3,若∠B+∠B′=90°,则△ABC与△A′B′C′的面积比为 _______。
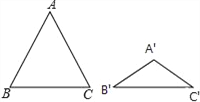
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD,BD分别平分∠CAB和∠CBA,相交于点D. 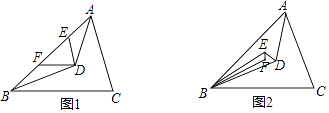
(1)如图1,过点D作DE∥AC,DF∥BC分别交AB于点E、F. ①若∠EDF=80°,则∠C为多少?
②若∠EDF=x°,证明:∠ADB=(90+ ![]() )°.
)°.
(2)如图2,若DE,BE分别平分∠ADB和∠ABD,且EF,BF分别平分∠BED和∠EBD,若∠BFE的度数是整数,求∠BFE至少是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列式子中去括号错误的是( )
A.5x﹣(x﹣2y)=5x﹣x+2y
B.2a2+(3a﹣b)=2a2+3a﹣b
C.(x﹣2y)﹣(x2﹣y2)=x﹣2y﹣x2+y2
D.3x2﹣3(x+6)=3x2﹣3x﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,两个完全相同的含30°角的Rt△ABC和Rt△AED叠放在一起,BC交DE于点O,AB交DE于点G,BC交AE于点F,且∠DAB=30°,以下三个结论:①AF⊥BC;②△ADG≌△AFC;③O为BC的中点;④AG=BG.其中正确的个数为( ) 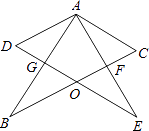
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
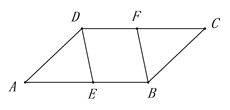
【题目】
(1)如图,在平行四边形ABCD中,已知点E在AB上,点F在CD上,且AE=CF.
求证:DE=BF
(2)如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=20°,求∠CDA的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com