
【题目】如图所示,两个完全相同的含30°角的Rt△ABC和Rt△AED叠放在一起,BC交DE于点O,AB交DE于点G,BC交AE于点F,且∠DAB=30°,以下三个结论:①AF⊥BC;②△ADG≌△AFC;③O为BC的中点;④AG=BG.其中正确的个数为( ) 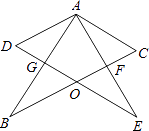
A.1
B.2
C.3
D.4
【答案】D
【解析】解:∵两块完全相同的含30°角的直角三角板叠放在一起,且∠DAB=30°. ∴∠CAF=30°,
∴∠GAF=60°,
∴∠AFB=90°,
∴AF丄BC正确,故①正确,
∵AD=AC,∠DAG=∠CAF,∠D=∠C=60°,
∴△ADG≌△ACF正确,故②正确,
∵△ADG≌△ACF,
∴AG=AF,
∵AO=AO,
∠AGO=∠AFO=90°,
∴△AGO≌△AFO,
∴∠OAF=30°,
∴∠OAC=60°,
∴AO=CO=AC,
∴BO=CO=AO,故③正确,
在Rt△AGE中,∵∠AGE=90°,∠E=30°,
∴AG= ![]() AE,
AE,
∵AB=AE,
∴AG= ![]() AB,
AB,
∴AG=GB,故④正确.
故选D.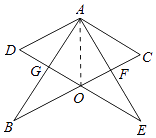


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
【题目】综合题。
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:CN∥AB.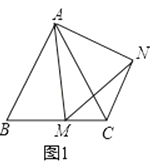
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论CN∥AB还成立吗?请说明理由.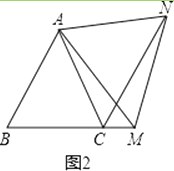
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l外不重合的两点A、B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:①作点B关于直线l的对称点B′;②连接AB′与直线l相交于点C,则点C为所求作的点.在解决这个问题时没有运用到的知识或方法是( )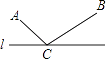
A.转化思想
B.三角形的两边之和大于第三边
C.两点之间,线段最短
D.三角形的一个外角大于与它不相邻的任意一个内角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为______

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京沈高铁赤峰至喀左段于2016年开工建设,天义镇路基桥墩建设初具规模,预计2019年运营,从赤峰出发经宁城至北京500公里,高铁运行速度将是现行普通客车平均速度的5倍,预计开通后,从赤峰出发,某高铁客运专列比普通客车晚3小时开出,但比普通客车早5小时到达北京,求两车的运行速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分) 已知双曲线y=![]() (x>0),直线l1:y﹣
(x>0),直线l1:y﹣![]() =k(x﹣
=k(x﹣![]() )(k<0)过定点F且与双曲线交于A,B两点,设A(x1,y1),B(x2,y2)(x1<x2),直线l2:y=﹣x+
)(k<0)过定点F且与双曲线交于A,B两点,设A(x1,y1),B(x2,y2)(x1<x2),直线l2:y=﹣x+![]() .
.
(1)若k =﹣1,求△OAB的面积S;
(2)若AB= ![]() ,求k的值;
,求k的值;
(3)设N(0,2![]() ),P在双曲线上,M在直线l2上且PM∥x轴,问在第二象限内是否存在一点Q,使得四边形QMPN是周长最小的平行四边形,若存在,请求出Q点的坐标。
),P在双曲线上,M在直线l2上且PM∥x轴,问在第二象限内是否存在一点Q,使得四边形QMPN是周长最小的平行四边形,若存在,请求出Q点的坐标。

查看答案和解析>>
科目:初中数学 来源: 题型:
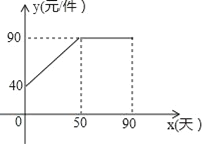
【题目】九年级某班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
时间x(天) | 1 | 30 | 60 | 90 |
每天销售量p(件) | 198 | 140 | 80 | 20 |
(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
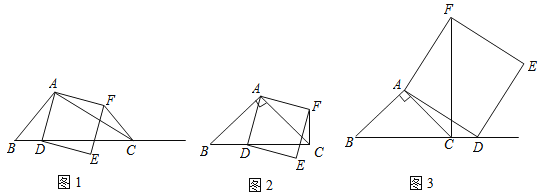
【题目】在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.如果AB=AC,∠BAC=90o,
(1)当点D在线段BC上时(与点B不重合),如图2,线段CF 、BD所在直线的位
置关系为 __________,线段CF 、BD的数量关系为 ;
(2)当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com