
【题目】如图是用棋子摆成的“上”字.

(1)依照此规律,第4个图形需要黑子、白子各多少枚?
(2)按照这样的规律摆下去,摆成第n个“上”字需要黑子、白子各多少枚?
(3)请探究第几个“上”字图形白子总数比黑子总数多15枚.
【答案】(1)黑子5枚,白子14枚;(2)黑子(n+1)枚,白子(3n+2)枚;(3)第7个.
【解析】
(1)根据已知得出黑棋子的变化规律为2,3,4…,白棋子为5,8,11…即可得出规律;
(2)用(1)中数据可以得出变化规律,摆成第n个“上”字需要黑子 n+1 个,白子3n+2 个;
(3)设第n个“上”字图形白子总数比黑子总数多15个,进而得出3n+2=(n+1)+15,求出即可.
解:(1)依照此规律,第4个图形需要黑子5枚,白子14枚.
(2)按照这样的规律摆下去,摆成第n个“上”字需要黑子(n+1)枚,白子(3n+2)枚.
(3)设第m个“上”字图形白子总数比黑子总数多15枚,
则3m+2=m+1+15,
解得m=7.
所以第7个“上”字图形白子总数比黑子总数多15枚.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
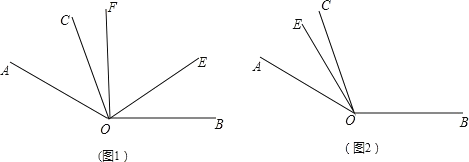
【题目】如图1,已知∠AOB=![]() ,∠AOC=
,∠AOC=![]() ,OE是∠AOB内部的一条射线,且OF平分∠AOE.
,OE是∠AOB内部的一条射线,且OF平分∠AOE.
(1)若∠EOB=![]() ,求∠COF的度数;
,求∠COF的度数;
(2)若∠COF=![]() ,求∠EOB的度数(用含n的式子表示);
,求∠EOB的度数(用含n的式子表示);
(3)当射线OE绕点O逆时针旋转到如图2的位置时,请把图补充完整;此时,∠COF与∠EOB有怎样的数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠的放在一个底面为长方形(长为a厘米,宽为b厘米)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )

A. 4a厘米B. 4b厘米C. 2(a+b)厘米D. 4(a-b)厘米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正整数1至2018按一定规律排列如下表:
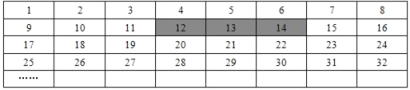
平移表中带阴影的方框,方框中三个数的和可能是( )
A. 2018 B. 2019 C. 2040 D. 2049
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y1=![]() 的图象与一次函数y2=
的图象与一次函数y2=![]() 的图象交于点A,B,点B的横坐标实数4,点P(1,m)在反比例函数y1=
的图象交于点A,B,点B的横坐标实数4,点P(1,m)在反比例函数y1=![]() 的图象上.
的图象上.
(1)求反比例函数的表达式;
(2)观察图象回答:当x为何范围时,y1>y2;
(3)求△PAB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
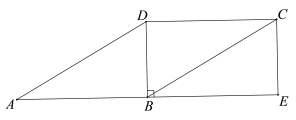
【题目】如图,在□ABCD中,∠ABD=90°,延长AB至点E,使BE=AB,连接CE.
(1)求证:四边形BECD是矩形;
(2)连接DE交BC于点F,连接AF,若CE=2,∠DAB=30°,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个自然数可以表示为三个连续奇数的和,那么我们就称这个数为“锦鲤数”,如:9=1+3+5,所以9是“锦鲤数”.
(1)请问21和35是不是“锦鲤数”,并说明理由;
(2)规定:![]()
![]() (其中
(其中![]() ,且
,且![]() 为自然数),是否存在一个“锦鲤数”
为自然数),是否存在一个“锦鲤数”![]() ,使得
,使得![]() 50=-3666.若存在,则求出
50=-3666.若存在,则求出![]() ,并把
,并把![]() 表示成3个连续的奇数和的形式,若不存在,请说明理由.
表示成3个连续的奇数和的形式,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为美化校园,安排甲、乙两个工程队进行绿化.已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在各自独立完成面积为400m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若绿化区域面积为1800m2,学校每天需付给甲队的绿化费用为0.4万元,每天需付给乙队的绿化费用为0.25万元,设安排甲队工作y天,绿化总费用为W万元.
①求W与y的函数关系式;
②要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com