
【题目】如图,反比例函数y1=![]() 的图象与一次函数y2=
的图象与一次函数y2=![]() 的图象交于点A,B,点B的横坐标实数4,点P(1,m)在反比例函数y1=
的图象交于点A,B,点B的横坐标实数4,点P(1,m)在反比例函数y1=![]() 的图象上.
的图象上.
(1)求反比例函数的表达式;
(2)观察图象回答:当x为何范围时,y1>y2;
(3)求△PAB的面积.

【答案】(1)反比例函数的表达式为y=![]() ;(2)x<﹣4或0<x<4时,y1>y2;(3)△PAB的面积为15.
;(2)x<﹣4或0<x<4时,y1>y2;(3)△PAB的面积为15.
【解析】
(1)利用一次函数求得B点坐标,然后用待定系数法求得反函数的表达式即可;
(2)观察图象可知,反函数的图象在一次函数图象上方的部分对应的自变量的取值范围就是不等式y1>y2的解;
(3)过点A作AR⊥y轴于R,过点P作PS⊥y轴于S,连接PO,设AP与y轴交于点C,由点A与点B关于原点对称,得出OA=OB,则S△AOP=S△BOP,即S△PAB=2S△AOP,再求出点P的坐标,利用待定系数法求得直线AP的函数解析式,得到点C的坐标,然后根据S△AOP=S△AOC+S△POC,即可求得结果.
(1)将x=4代入y2=![]() 得:y=1,
得:y=1,
∴B(4,1),
∴k=xy=4×1=4,
∴反比例函数的表达式为y=![]() ;
;
(2)由正比例函数和反比例函数的对称性可知点A的横坐标为﹣4.
∵y1>y2,
∴反比例函数图象位于正比例函数图象上方,
∴x<﹣4或0<x<4;
(3)过点A作AR⊥y轴于R,过点P作PS⊥y轴于S,连接PO,
设AP与y轴交于点C,如图,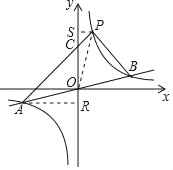
∵点A与点B关于原点对称,
∴OA=OB,
∴S△AOP=S△BOP,
∴S△PAB=2S△AOP,
y1=![]() 中,当x=1时,y=4,
中,当x=1时,y=4,
∴P(1,4),
设直线AP的函数关系式为y=mx+n,
把点A(﹣4,﹣1)、P(1,4)代入y=mx+n,
得![]() ,
,
解得m=3,n=1,
故直线AP的函数关系式为y=x+3,
则点C的坐标(0,3),OC=3,
∴S△AOP=S△AOC+S△POC
=![]() OCAR+
OCAR+![]() OCPS
OCPS
=![]() ×3×4+
×3×4+![]() ×3×1
×3×1
=![]() ,
,
∴S△PAB=2S△AOP=15.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,线段AB=24,动点P从A出发,以每秒2个单位的速度沿射线AB运动,运动时间为t秒(t>0),点M为AP的中点.
![]()
(1)当点P在线段AB上运动时.当t为多少时,AM=6.
(2)当点P在AB延长线上运动时,点N为BP的中点,求出线段MN的长度.
(3)在P点的运动过程中,点N为BP的中点,是否存在这样的t的值,使M、N、B三点中的一个点是以其余两点为端点的线段的中点,若有,请求出t的值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师在黑板上出了一道解方程的题![]() ,小虎马上举手,要求到黑板上去做,他是这样做的:
,小虎马上举手,要求到黑板上去做,他是这样做的:
5(3x-1)=2(4x+2)-1①,
15x-5=8x+4-1②,
15x-8x=4-1+5③
7x④,
x=![]() ⑤
⑤
老师说:小虎解一元一次方程的一般步骤都知道,但没有掌握好,因此解题出现了错误,请指出他的错步及错误原因: ,方程的正确的解是x= .
然后,你自己细心的解下面的方程:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
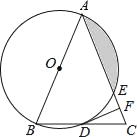
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E.过点D作DF⊥AC交AC于点F.
(1)求证:DF是⊙O的切线;
(2)若⊙O的半径为8,∠CDF=22.5°,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则下列结论:①4ac﹣b2<0;②2a﹣b=0;③a+b+c<0;④点M(x1,y1)、N(x2,y2)在抛物线上,若x1<x2<﹣1,则y1>y2,⑤abc>0.其中正确结论的个数是( )
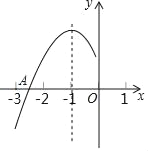
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用棋子摆成的“上”字.

(1)依照此规律,第4个图形需要黑子、白子各多少枚?
(2)按照这样的规律摆下去,摆成第n个“上”字需要黑子、白子各多少枚?
(3)请探究第几个“上”字图形白子总数比黑子总数多15枚.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下图,解答下列问题.

(1)图中的小圆圈被折线隔开分成六层,第一层有1个小圆圈,第二层有3个圆圈,第三层有5个圆圈,…,第六层有11个圆圈.如果要你继续画下去,那么第八层有几个小圆圈?第n层呢?
(2)某一层上有65个圆圈,这是第几层?
(3)数图中的圆圈个数可以有多种不同的方法.
比如:前两层的圆圈个数和为(1+3)或22,
由此得,1+3=22.同样,
由前三层的圆圈个数和得:1+3+5=32.
由前四层的圆圈个数和得:1+3+5+7=42.
由前五层的圆圈个数和得:1+3+5+7+9=52.…
根据上述请你计算:1+3+5+…+99的和
(4)猜测:从1开始的n个连续奇数之和是多少?用公式把它表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B、C是数轴上三点,O为原点.点C对应的数为6,BC=4,AB=12.
(1)求点A、B对应的数;
(2)动点P、Q分别同时从A、C出发,分别以每秒6个单位和3个单位的速度沿数轴正方向运动.M为AP的中点,N在CQ上,且CN=![]() CQ,设运动时间为t(t>0).
CQ,设运动时间为t(t>0).
①求点M、N对应的数(用含t的式子表示); ②t为何值时,OM=2BN.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对x,y定义一种新运算T,规定:T(x,y)=![]() (其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=
(其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=![]() =b.
=b.
(1)已知T(1,﹣1)=﹣2,T(4,2)=1.
①求a,b的值;
②若关于m的不等式组![]() 恰好有3个整数解,求实数p的取值范围;
恰好有3个整数解,求实数p的取值范围;
(2)若T(x,y)=T(y,x)对任意实数x,y都成立(这里T(x,y)和T(y,x)均有意义),则a,b应满足怎样的关系式?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com