
【题目】在图1﹣﹣图4中,菱形ABCD的边长为3,∠A=60°,点M是AD边上一点,且DM= ![]() AD,点N是折线AB﹣BC上的一个动点.
AD,点N是折线AB﹣BC上的一个动点.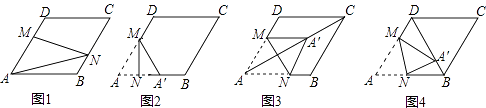
(1)如图1,当N在BC边上,且MN过对角线AC与BD的交点时,则线段AN的长度为 .
(2)当点N在AB边上时,将△AMN沿MN翻折得到△A′MN,如图2,
①若点A′落在AB边上,则线段AN的长度为;
②当点A′落在对角线AC上时,如图3,求证:四边形AM A′N是菱形;
③当点A′落在对角线BD上时,如图4,求 ![]() 的值.
的值.
【答案】
(1)![]()
(2)1,解:②在菱形ABCD中,AC平分∠DAB,∵∠DAB=60°,∴∠DAC=∠CAB=30°,∵△AMN沿MN翻折得到△A′MN,∴AC⊥MN,AM=A′M,AN=A′N,;∴∠AMN=∠ANM=60°,∴AM=AN,∴AM=A′M=AN=A′N,∴四边形AM A′N是菱形;,③在菱形ABCD中,AB=AD,∴∠ADB=∠ABD=60°,∴∠BA′M=∠DMA′+∠ADB,∴A′M=AM=2,∠NA′M=∠A=60°,∴∠NA′B=∠DMA′,∴△DMA′∽△BA′N,∴ ![]() =
= ![]() ,∵MD=
,∵MD= ![]() AD=1,A′M=2,∴
AD=1,A′M=2,∴ ![]() =
= ![]()
【解析】解:(1)如图1,

过点N作NG⊥AB于G,
∵四边形ABCD是菱形,
∴AD∥BC,OD=OB,
∴ ![]() =
= ![]() =1,
=1,
∴BN=DM= ![]() AD=1,
AD=1,
∵∠DAB=60°,
∴∠NBG=60°
∴BG= ![]() ,GN=
,GN= ![]() ,
,
∴AN= ![]() =
= ![]() =
= ![]() ;
;
故答案为: ![]() ;
;
( 2 )①当点A′落在AB边上,则MN为AA′的中垂线,
∵∠DAB=60°AM=2,
∴AN= ![]() AM=1,
AM=1,
故答案为:1;
(1)过点N作NG⊥AB于G,构造直角三角形,根据菱形的性质得出AD∥BC,OD=OB,∠NBG=60° ,根据平行线分线段成比例定理得出DM∶BN=OD∶OB=1,从而得出BN=DM=1 ,利用含30°的直角三角形的边的关系得出BG、GN的长,利用勾股定理解决问题;
(2)①利用线段中垂线的性质得到MN⊥AA',利用含30°的直角三角形的边的关系得出AN的长;
②利用菱形的性质得到对角线平分每一组对角,得到∠DAC=∠CAB=30°,根据翻折的性质得到AC⊥MN,AM=A′M,AN=A′N,∠AMN=∠ANM=60°,AM=AN,AM=A′M=AN=A′N,四边形AM A′N是菱形
③根据菱形的性质得到AB=AD,∠ADB=∠ABD=60°,求得∠NA′M=∠DMA′+∠ADB,证得A′M=AM=2,∠NA′M=∠A=60°,得到∠NA′B=∠DMA′,从而判断出△DMA′∽△BA′N,利用相似三角形对应边成比例得到结果.


科目:初中数学 来源: 题型:
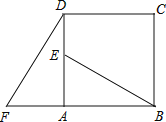
【题目】如图,四边形ABCD是正方形,△ADF按顺时针方向旋转一定角度后得到△ABE,
若AF=4,AB=7.
(1)旋转中心为______;旋转角度为______;
(2)DE的长度为______;
(3)指出BE与DF的位置关系如何?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车厂改进生产工艺后,每天生产的汽车比原来每天生产的汽车多6辆,那么现在15天的产量就超过了原来20天的产量,若设原来每天能生产x辆,则可列不等式为( )
A. 15(x+6)>20xB. 15x>20(x+6)C. 15x>20(x-6)D. 15(x+6)≥20x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用不等式的基本性质求下列不等式的解集,并说出变形的依据.
(1)若x+2 012>2 013,则x__________;(______________________________)
(2)若2x>-![]() ,则x__________;(______________________________)
,则x__________;(______________________________)
(3)若-2x>-![]() ,则x__________;(______________________________)
,则x__________;(______________________________)
(4)若-![]() >-1,则x__________.(______________________________)
>-1,则x__________.(______________________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
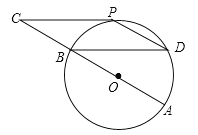
【题目】如图,⊙O的直径AB=12cm,C为AB延长线上一点,CP与⊙O相切于点P,过点B作弦BD∥CP,连接PD.
(1)求证:点P为![]() 的中点;
的中点;
(2)若∠C=∠D,求四边形BCPD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在西部大开发中,为了改善生态环境,鄂西政府决定绿化荒地,计划第1年先植树1.5万亩,以后每年比上一年增加1万亩,结果植树总数是时间(年)的一次函数,则这个一次函数的图象是( )
A.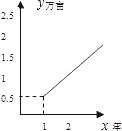
B.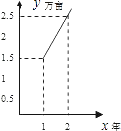
C.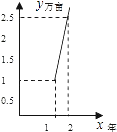
D.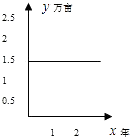
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com