
【题目】如图,在方格纸中,每个小正方形的边长为1个单位长度,△ABC的顶点都在格点上.

(1)画出△ABC先向右平移6格,再向上平移1格所得的△A′B′C′;
(2)画出△ABC的AB边上的中线CD和高线CE;
(3)求△ABC的面积.
科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,我市居民使用自来水计费方式实施阶梯水价,具体标准见表1,表2分别是小明、小丽、小斌、小宇四家2017年的年用水量和缴纳水费情况.
表1:大连市居民自来水实施阶梯水价标准情况:

表2:四个家庭2017年的年用水量和缴纳水费情况:
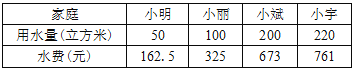
请你根据表1、表2提供的数据回答下列问题:
(1)表1中的![]() __________,
__________,![]() _____________;
_____________;
(2)小颖家2017年使用自来水共缴纳水费827元,则她家2017年的年用水量是多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在⊙O上,∠CAB的平分线交⊙O于点D,过点D作AC的垂线交AC的延长线于点E,连接BC交AD于点F.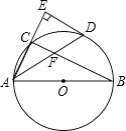
(1)猜想ED与⊙O的位置关系,并证明你的猜想;
(2)若AB=6,AD=5,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形纸片ABCD中,AB=12,BC=16.将矩形纸片ABCD折叠,使点B与点D重合,点A折叠至点E处,GH为折痕,连接BG.
(1)△DGH是等腰三角形吗?请说明你的理由.
(2)求线段AG的长;
(3)求折痕GH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
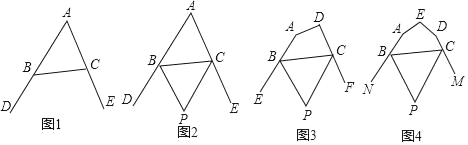
【题目】(1)如图1,在△ABC中,∠DBC与∠ECB分别为△ABC的两个外角,若∠A=60°,∠DBC+∠ECB多少度;
(2)如图2,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有怎样的数量关系?为什么?
(3)如图3,在四边形ABCD中,BP、CP分别平分外角∠EBC、∠FCB,∠P与∠A+∠D有怎样的数量关系?为什么?
(4)如图4,在五边形ABCDE中,BP、CP分别平分外角∠NBC、∠MCB,∠P与∠A+∠D+∠E有怎样的数量关系?(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列解题过程,然后回答问题:
解方程: ![]()
解:①当![]() ≥0时,原方程可化为:
≥0时,原方程可化为: ![]() ,解得
,解得![]() ;
;
②当![]() <0时,原方程可化为:
<0时,原方程可化为: ![]() ,解得
,解得![]() ;
;
所以原方程的解是![]() 或
或![]()
(1)解方程: ![]()
(2)探究:当![]() 为何值时,方程
为何值时,方程![]() ①无解;②只有一个解;③有两个解。
①无解;②只有一个解;③有两个解。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=4cm,点E、F同时从C点出发,以1cm/s的速度分别沿CB﹣BA、CD﹣DA运动,到点A时停止运动.设运动时间为t(s),△AEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )
A.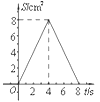
B.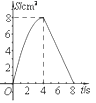
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好改善河流的水质,治污公司决定购买10台污水处理设备![]() 现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
A型 | B型 | |
价格 | a | b |
处理污水量 | 240 | 200 |
![]() 求a,b的值;
求a,b的值;
![]() 治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
![]() 在
在![]() 的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com