
【题目】已知:如图,A、B、C为⊙O上的三个点,⊙O的直径为4cm,∠ACB=45°,求AB的长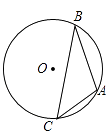
【答案】解:连接OA,OB,

∵∠ACB=45°,
∴∠AOB=2∠ACB=90°,
∵⊙O的直径为4cm,
∴OA=OB=2cm,
∴AB= ![]() (cm)
(cm)
【解析】抓住题中根据的已知条件,圆周角∠ACB=45°,根据圆周角定理即可添加辅助线构造圆心角是直角,因此连接OA、OB,先求出半径的长,再利用勾股定理求出AB的长。
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对圆周角定理的理解,了解顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.


科目:初中数学 来源: 题型:
【题目】如图,∠BAC=90°,AD⊥BC,垂足为点 D.下列说法中:①∠B的余角只有∠BAD;②∠B=∠C;③线段 AB 的长度表示点 B 到直线 AC 的距离;④AB·AC=BC·AD;一定正确的有( )
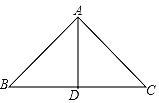
A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2012年6月1日起,国家实施了中央财政补贴条例支持高效节能电器的推广使用,某款定速空调在条例实施后,每购买一台,客户可获财政补贴200元,若同样用11万元所购买的此款空调数台,条例实施后比实施前多10%.求条例实施前此款空调的单价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,把△ABC沿DE折叠,使点A落在点A’处,试探索∠1+∠2与∠A的关系.(证明).
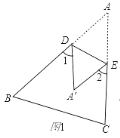
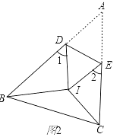
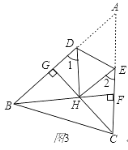
(2)如图2,BI平分∠ABC,CI平分∠ACB,把△ABC折叠,使点A与点I重合,若∠1+∠2=130°,求∠BIC的度数;
(3)如图3,在锐角△ABC中,BF⊥AC于点F,CG⊥AB于点G,BF、CG交于点H,把△ABC折叠使点A和点H重合,试探索∠BHC与∠1+∠2的关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期学习了分式方程的解法,下面是晶晶同学的解题过程:
解方程 ![]()
解:整理,得: ![]() …………………………第①步
…………………………第①步
去分母,得: ![]() …………………………第②步
…………………………第②步
移项,得: ![]() ……………………… 第③步
……………………… 第③步
合并同类项,得: ![]() ……………………… 第④步
……………………… 第④步
系数化1,得: ![]() …………………………第⑤步
…………………………第⑤步
检验:当![]() 时,
时,![]()
所以原方程的解是![]() . ………………………第⑥步
. ………………………第⑥步
上述晶晶的解题过程从第_____步开始出现错误,错误的原因是_________________.请你帮晶晶改正错误,写出完整的解题过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,以平行四边形ABCD的顶点A为圆心,AB为半径作圆,分别交BC,AD于E,F两点,交BA的延长于G,判断弧EF和弧FG是否相等,并说明理由。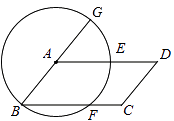
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是春运期间的一个回家场景。一种拉杆式旅行箱的示意图如图所示,箱体长AB=50cm,拉杆最大伸长距离BC=30cm,点A到地面的距离AD=8cm,旅行箱与水平面AE成60°角,求拉杆把手处C到地面的距离(精确到1cm).(参考数据: ![]() )
)
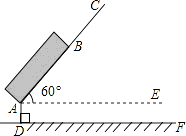
查看答案和解析>>
科目:初中数学 来源: 题型:
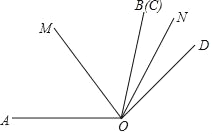
【题目】如图,∠AOB=α,∠COD=β(α>β),OC与OB重合,OD在∠AOB外,射线OM、ON分别是∠AOC、∠BOD的角平分线.
(1)①若α=100°,β=60°,则∠MON等于多少;
②在①的条件下∠COD绕点O逆时针旋转n°(0<n<100(且n≠60)时,求∠MON的度数;
(2)直接写出∠COD绕点O逆时针旋转n°(0<n<360)时∠MON的值(用含α、β的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸中,每个小正方形的边长为1个单位长度,△ABC的顶点都在格点上.

(1)画出△ABC先向右平移6格,再向上平移1格所得的△A′B′C′;
(2)画出△ABC的AB边上的中线CD和高线CE;
(3)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com