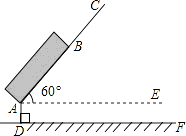
【题目】如图是春运期间的一个回家场景。一种拉杆式旅行箱的示意图如图所示，箱体长AB=50cm，拉杆最大伸长距离BC=30cm，点A到地面的距离AD=8cm，旅行箱与水平面AE成60°角，求拉杆把手处C到地面的距离（精确到1cm）．（参考数据： 
）
科目：初中数学 来源： 题型：
【题目】如图，在长方形ABCD中，点M为CD中点，将△MBC沿BM翻折至△MBE，若∠AME ＝ α，∠ABE ＝ β，则 α 与 β 之间的数量关系为( )
A. α＋3β＝180° B. β－α＝20° C. α＋β＝80° D. 3β－2α＝90°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，E是等边三角形ABC的边AB所在直线上一点，D是边BC所在直线上一点，且D与C不重合，若EC＝ED．则称D为点C关于等边三角形ABC的反称点，点E称为反称中心．
在平面直角坐标系xOy中，
（1）已知等边三角形AOC的顶点C的坐标为（2，0），点A在第一象限内，反称中心E在直线AO上，反称点D在直线OC上．
①如图2，若E为边AO的中点，在图中作出点C关于等边三角形AOC的反称点D，并直接写出点D的坐标： ；
②若AE＝2，求点C关于等边三角形AOC的反称点D的坐标；
（2）若等边三角形ABC的顶点为B（n，0），C（n+1，0），反称中心E在直线AB上，反称点D在直线BC上，且2≤AE＜3．请直接写出点C关于等边三角形ABC的反称点D的横坐标t的取值范围： （用含n的代数式表示）．
查看答案和解析>>
科目：初中数学 来源： 题型：
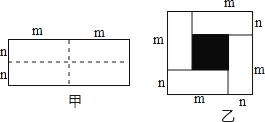
【题目】已知图甲是一个长为2m，宽为2n的长方形，沿图中虚线用剪刀均剪成四个小长方形，然后拼成如图乙所示的一个大正方形．
（1）你认为图乙中的阴影部分的正方形的边长＝ ；
（2）请用两种不同的方法求图乙中阴影部分的面积：
方法一：
方法二：
（3）观察图乙，请你写出下列代数式之间的等量关系：
（m+n）2、（m﹣n）2、mn
．
（4）根据（3）题中的等量关系，解决如下问题：若a+b＝8，ab＝7，求a﹣b的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】先化简，再求值：a+
，其中a=1007.如图是小亮和小芳的解答过程.
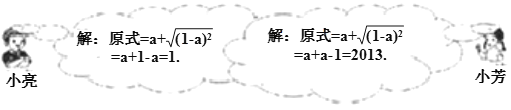
(1)_________的解法是错误的；
(2)错误的原因在于未能正确地运用二次根式的性质：_________；
(3)先化简，再求值：a+2
，其中a=-2007.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我国明代珠算家程大位的名著《直指算法统宗》里有一道著名算题：“一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚各几丁？”意思是：有100个和尚分100个馒头，如果大和尚1人分3个，小和尚3人分1个，正好分完，试问大、小和尚各多少人？设大和尚有x人，依题意列方程得（ ）
A. 
+3（100﹣x）＝100 B. ﹣3（100﹣x）＝100
C. 3x﹣
＝100 D. 3x+＝100
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了鼓励市民节约用水，我市居民使用自来水计费方式实施阶梯水价，具体标准见表1，表2分别是小明、小丽、小斌、小宇四家2017年的年用水量和缴纳水费情况．
表1：大连市居民自来水实施阶梯水价标准情况：
表2：四个家庭2017年的年用水量和缴纳水费情况：
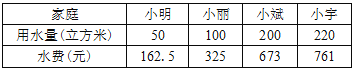
请你根据表1、表2提供的数据回答下列问题：
（1）表1中的
__________，
_____________；
（2）小颖家2017年使用自来水共缴纳水费827元，则她家2017年的年用水量是多少立方米？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】先阅读下列解题过程，然后回答问题：
解方程： 
解：①当
≥0时，原方程可化为： 
，解得
；
②当
＜0时，原方程可化为： 
，解得
；
所以原方程的解是
或
（1）解方程： 
（2）探究：当
为何值时，方程
①无解；②只有一个解；③有两个解。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
