
【题目】如图,在长方形ABCD中,点M为CD中点,将△MBC沿BM翻折至△MBE,若∠AME = α,∠ABE = β,则 α 与 β 之间的数量关系为( )

A. α+3β=180° B. β-α=20° C. α+β=80° D. 3β-2α=90°
【答案】D
【解析】
直接利用平行线的性质结合翻折变换的性质得出△ADM≌△BCM(SAS),进而利用直角三角形的性质得出答案.
∵M为CD中点,
∴DM=CM,
在△ADM和△BCM中
∵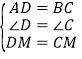 ,
,
∴△ADM≌△BCM(SAS),
∴∠AMD=∠BMC,AM=BM
∴∠MAB=∠MBA
∵将点C绕着BM翻折到点E处,
∴∠EBM=∠CBM,∠BME=∠BMC=∠AMD
∴∠DME=∠AMB
∴∠EBM=∠CBM=![]() (90°-β)
(90°-β)
∴∠MBA=![]() (90°-β)+ β=
(90°-β)+ β=![]() (90°+β)
(90°+β)
∴∠MAB=∠MBA=![]() (90°+β)
(90°+β)
∴∠DME=∠AMB=180°-∠MAB-∠MBA=90°-β
∵长方形ABCD中,
∴CD∥AB
∴∠DMA=∠MAB=![]() (90°+β)
(90°+β)
∴∠DME+∠AME=∠ABE+∠MBE
∵∠AME=α,∠ABE=β,
∴90°-β+α=β+![]() (90°-β)
(90°-β)
∴3β-2α=90°
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,∠BAC=90°,AD⊥BC,垂足为点 D.下列说法中:①∠B的余角只有∠BAD;②∠B=∠C;③线段 AB 的长度表示点 B 到直线 AC 的距离;④AB·AC=BC·AD;一定正确的有( )
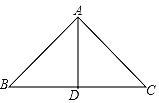
A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于![]() 轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C和△A2B2C2,它们是否关于某直线对称?若是,请用实线条画出对称轴。

查看答案和解析>>
科目:初中数学 来源: 题型:
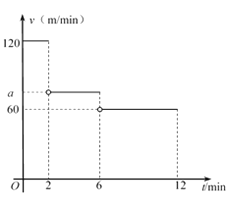
【题目】小明从家出发,沿一条直道散步到离家450 m的邮局,经过一段时间原路返回,刚好在第12 min回到家中.设小明出发第t min时的速度为v m/min,v与t之间的函数关系如图所示(图中的空心圈表示不包含这一点).
(1)小明出发第2 min时离家的距离为 m;
(2)当2< t ≤6时,求小明的速度a;
(3)求小明到达邮局的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)3x3x9﹣2xx3x8
(2)﹣12+20160+(![]() )2017×(﹣4)2018
)2017×(﹣4)2018
(3)(x+4)(x﹣4)﹣(x﹣2)2
(4)ab(a+b)﹣(a﹣b)(a2+b2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2012年6月1日起,国家实施了中央财政补贴条例支持高效节能电器的推广使用,某款定速空调在条例实施后,每购买一台,客户可获财政补贴200元,若同样用11万元所购买的此款空调数台,条例实施后比实施前多10%.求条例实施前此款空调的单价.
查看答案和解析>>
科目:初中数学 来源: 题型:
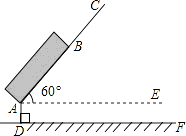
【题目】如图是春运期间的一个回家场景。一种拉杆式旅行箱的示意图如图所示,箱体长AB=50cm,拉杆最大伸长距离BC=30cm,点A到地面的距离AD=8cm,旅行箱与水平面AE成60°角,求拉杆把手处C到地面的距离(精确到1cm).(参考数据: ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com