
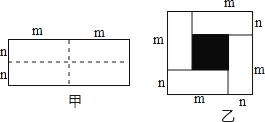
【题目】已知图甲是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均剪成四个小长方形,然后拼成如图乙所示的一个大正方形.
(1)你认为图乙中的阴影部分的正方形的边长= ;
(2)请用两种不同的方法求图乙中阴影部分的面积:
方法一:
方法二:
(3)观察图乙,请你写出下列代数式之间的等量关系:
(m+n)2、(m﹣n)2、mn
.
(4)根据(3)题中的等量关系,解决如下问题:若a+b=8,ab=7,求a﹣b的值.
【答案】(1)m﹣n;(2)方法一:(m﹣n)2,方法二:(m+n)2﹣4mn;(3)(m﹣n)2=(m+n)2﹣4mn;(4)a﹣b=±6.
【解析】
(1)根据图乙中的阴影部分的正方形的边长等于小长方形的长减去宽进行判断;
(2)图乙中阴影部分的面积既可以用边长的平方进行计算,也可以用大正方形的面积减去四个小长方形的面积进行计算;
(3)根据(m﹣n)2和(m+n)2﹣4mn表示同一个图形的面积进行判断;
(4)根据(a﹣b)2=(a+b)2﹣4ab,进行计算即可得到a﹣b的值.
(1)由题可得,图乙中的阴影部分的正方形的边长等于m﹣n;
故答案为:m﹣n;
(2)方法一:
图乙中阴影部分的面积=(m﹣n)2
方法二:
图乙中阴影部分的面积=(m+n)2﹣4mn;
故答案为:(m﹣n)2,(m+n)2﹣4mn;
(3)∵(m﹣n)2和(m+n)2﹣4mn表示同一个图形的面积;
∴(m﹣n)2=(m+n)2﹣4mn;
故答案为:(m﹣n)2=(m+n)2﹣4mn;
(4)∵(a﹣b)2=(a+b)2﹣4ab,
而a+b=8,ab=7,
∴(a﹣b)2=82﹣4×7=64﹣28=36,
∴a﹣b=±6.



科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于![]() 轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C和△A2B2C2,它们是否关于某直线对称?若是,请用实线条画出对称轴。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,点![]() 为坐标原点,点
为坐标原点,点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在
在![]() 轴的负半轴上,点
轴的负半轴上,点![]() 在
在![]() 轴正半轴上,
轴正半轴上,![]() ,梯形
,梯形![]() 的面积为
的面积为![]() ,
,![]() ,
,![]() .
.
(1)求点![]() ,
,![]() 的坐标;
的坐标;
(2)点![]() 从点
从点![]() 出发以
出发以![]() 个单位/秒的速度沿
个单位/秒的速度沿![]() 向终点
向终点![]() 运动,同时,点
运动,同时,点![]() 从点
从点![]() 出发以
出发以![]() 个单位秒的速度沿
个单位秒的速度沿![]() 向终点
向终点![]() 运动,设点
运动,设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长为
的长为![]() ,用含
,用含![]() 的关系式表示
的关系式表示![]() ,并直接写出相应的
,并直接写出相应的![]() 范围.
范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期学习了分式方程的解法,下面是晶晶同学的解题过程:
解方程 ![]()
解:整理,得: ![]() …………………………第①步
…………………………第①步
去分母,得: ![]() …………………………第②步
…………………………第②步
移项,得: ![]() ……………………… 第③步
……………………… 第③步
合并同类项,得: ![]() ……………………… 第④步
……………………… 第④步
系数化1,得: ![]() …………………………第⑤步
…………………………第⑤步
检验:当![]() 时,
时,![]()
所以原方程的解是![]() . ………………………第⑥步
. ………………………第⑥步
上述晶晶的解题过程从第_____步开始出现错误,错误的原因是_________________.请你帮晶晶改正错误,写出完整的解题过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上的任意一动点,点
边上的任意一动点,点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,直线
对称,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
(1)求![]() 边上的高;
边上的高;
(2)当![]() 为何值时,△
为何值时,△![]() 与△
与△![]() 重叠部分的面积最大,并求出最大值;
重叠部分的面积最大,并求出最大值;
(3)连接![]() ,当
,当![]() 为直角三角形时,求
为直角三角形时,求![]() 的度数.
的度数.



查看答案和解析>>
科目:初中数学 来源: 题型:
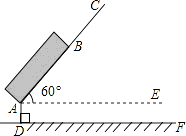
【题目】如图是春运期间的一个回家场景。一种拉杆式旅行箱的示意图如图所示,箱体长AB=50cm,拉杆最大伸长距离BC=30cm,点A到地面的距离AD=8cm,旅行箱与水平面AE成60°角,求拉杆把手处C到地面的距离(精确到1cm).(参考数据: ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】麒麟区第七中学现有一块空地ABCD如图所示,现计划在空地上种草皮,经测量,∠B=90°,AB=3m,BC=4m,CD=13m,AD=12m.

(1)求出空地ABCD的面积?
(2)若每种植1平方米草皮需要300元,问总共需投入多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com