
【题目】如图,在平面直角坐标系xOy中,⊙A与y轴相切于点B(0, ![]() ),与x轴相交于M,N两点,如果点M的坐标为(
),与x轴相交于M,N两点,如果点M的坐标为( ![]() ,0),求点N的坐标
,0),求点N的坐标
【答案】解:连接AB、AM、过A作AC⊥MN于C,设⊙A的半径是R,

∵⊙A与y轴相切于B,
∴AB⊥y轴,
∵点B(0, ![]() ),与x轴相交于M、N两点,点M的坐标为(
),与x轴相交于M、N两点,点M的坐标为( ![]() ,0),
,0),
∴AB=AM=R,CM=R- ![]() ,AC=
,AC= ![]() ,MN=2CM,
,MN=2CM,
由勾股定理得:R2=(R- ![]() )2+(
)2+( ![]() )2,
)2,
R=2.5,
∴CM=CN=2.5- ![]() =2,
=2,
∴ON= ![]() +2+2=4
+2+2=4 ![]() ,
,
即N的坐标是(4 ![]() ,0).
,0).
【解析】要求点N的坐标,就需求出MN的长,因此过A作AC⊥MN于C,连接AB、AM、先由点B的坐标,就可求出AC的长,AB=OC=R,由点M的坐标就可求出OM的长,表示出MC的长,根据勾股定理求出R的长,即可求出MN的长,从而得出点N的坐标。
【考点精析】根据题目的已知条件,利用勾股定理的概念和垂径定理的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.


科目:初中数学 来源: 题型:
【题目】某商场销售A,B两种品牌的教学设备,这两种教学设备的进价和售价如下表所示:
A | B | |
进价(万元/套) | 1.5 | 1.2 |
售价(万元/套) | 1.65 | 1.4 |
该商场计划购进两种教学设备若干套,共需66万元,全部销售后可获毛利润9万元。
(毛利润=(售价 - 进价)×销售量)
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少数量的1.5倍。若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:线段AB=40cm.
(1)如图①,点P沿线段AB自点A向点B以3厘米/秒运动,同时点Q线段BA自B点向点A以5厘米/秒运动,问经过几秒后P、Q相遇?
(2)几秒钟后,P、Q相距16厘米?
(3)如图②,AO=PO=8厘米,∠POB=40°,点P绕点O以20度/秒的速度顺时针旋转一周停止,同时点Q沿直线BA自B点向点A运动,假若P、Q两点能相遇,求Q运动的速度.
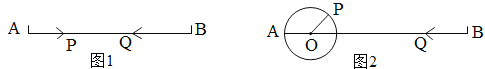
查看答案和解析>>
科目:初中数学 来源: 题型:
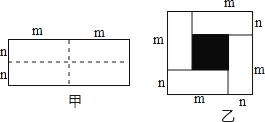
【题目】已知图甲是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均剪成四个小长方形,然后拼成如图乙所示的一个大正方形.
(1)你认为图乙中的阴影部分的正方形的边长= ;
(2)请用两种不同的方法求图乙中阴影部分的面积:
方法一:
方法二:
(3)观察图乙,请你写出下列代数式之间的等量关系:
(m+n)2、(m﹣n)2、mn
.
(4)根据(3)题中的等量关系,解决如下问题:若a+b=8,ab=7,求a﹣b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国明代珠算家程大位的名著《直指算法统宗》里有一道著名算题:“一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?”意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,试问大、小和尚各多少人?设大和尚有x人,依题意列方程得( )
A. ![]() +3(100﹣x)=100 B.
+3(100﹣x)=100 B. ![]() ﹣3(100﹣x)=100
﹣3(100﹣x)=100
C. 3x﹣![]() =100 D. 3x+
=100 D. 3x+![]() =100
=100
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,A、B两点在数轴上对应的数分别为﹣12和4.
(1)直接写出A、B两点之间的距离;
(2)若在数轴上存在一点P,使得AP=![]() PB,求点P表示的数.
PB,求点P表示的数.

(3)如图2,现有动点P、Q,若点P从点A出发,以每秒5个单位长度的速度沿数轴向右运动,同时点Q从点B出发,以每秒2个单位长度的速度沿数轴向左运动,当点Q到达原点O后立即以每秒3个单位长度的速度沿数轴向右运动,求:当OP=4OQ时的运动时间t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直线y=3x+3与x轴交于C点,与y轴交于A点,B点在x轴上,△OAB是等腰直角三角形.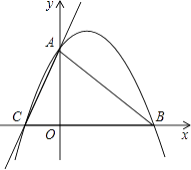
(1)求过A、B、C三点的抛物线的解析式;
(2)若直线CD∥AB交抛物线于D点,求D点的坐标;
(3)若P点是抛物线上的动点,且在第一象限,那么△PAB是否有最大面积?若有,求出此时P点的坐标和△PAB的最大面积;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用直尺和圆规画一个角等于已知角,是运用了“全等三角形的对应角相等”这一性质,其全等的依据是( )

A.SAS B.ASA C.AAS D.SSS
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com