Question

【题目】已知：如图，直线y=3x+3与x轴交于C点，与y轴交于A点，B点在x轴上，△OAB是等腰直角三角形．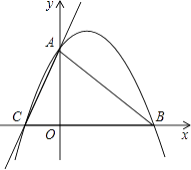

（1）求过A、B、C三点的抛物线的解析式；
（2）若直线CD∥AB交抛物线于D点，求D点的坐标；
（3）若P点是抛物线上的动点，且在第一象限，那么△PAB是否有最大面积？若有，求出此时P点的坐标和△PAB的最大面积；若没有，请说明理由．

Answer 1

【答案】
（1）解：令y=3x+3=0得：x=﹣1，

故点C的坐标为（﹣1，0）；

令x=0得：y=3x+3=3×0+3=3

故点A的坐标为（0，3）；

∵△OAB是等腰直角三角形．

∴OB=OA=3，

∴点B的坐标为（3，0），

设过A、B、C三点的抛物线的解析式y=ax2+bx+c，

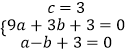
解得：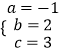

∴解析式为：y=﹣x2+2x+3

（2）解：设直线AB的解析式为y=kx+b，

∴

解得：

∴直线AB的解析式为：y=﹣x+3

∵线CD∥AB

∴设直线CD的解析式为y=﹣x+b

∵经过点C（﹣1，0），

∴﹣（﹣1）+b=0

解得：b=﹣1，

∴直线CD的解析式为：y=﹣x﹣1，

令﹣x﹣1=﹣x2+2x+3，

解得：x=﹣1，或x=4，

将x=4代入y=﹣x2+2x+3=﹣16+2×4+3=﹣5，

∴点D的坐标为：（4，﹣5）

（3）解：存在．如图1所示，设P（x，y）是第一象限的抛物线上一点，

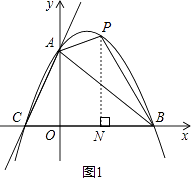
过点P作PN⊥x轴于点N，则ON=x，PN=y，BN=OB﹣ON=3﹣x．

S△ABP=S梯形PNOA+S△PNB﹣S△AOB

= （OA+PN）ON+ PNBN﹣ OAOB

= （3+y）x+ y（3﹣x）﹣ ×3×3

= （x+y）﹣ ，

∵P（x，y）在抛物线上，∴y=﹣x2+2x+3，代入上式得：

S△PAB= （x+y）﹣ =﹣ （x2﹣3x）=﹣ （x﹣ ）2+ ，

∴当x= 时，S△PAB取得最大值．

当x= 时，y=﹣x2+2x+3= ，

∴P（ ， ）．

所以，在第一象限的抛物线上，存在一点P，使得△ABP的面积最大；

P点的坐标为（ ， ），最大值为：

【解析】（1）先求出直线AC与x轴、y轴的交点的坐标，就可得出点A、C的坐标，再根据△OAB是等腰直角三角形．得出OA=OB，得出点B的坐标，再利用待定系数法就可求出过A、B、C三点的抛物线的解析式。
（2）先利用待定系数法求出直线AB的函数解析式，再根据CD∥AB，可知直线CD的解析式和直线AB的解析式中k值相等，再把点C的坐标代入即可求出直线CD的函数解析式，然后由抛物线的解析式和直线CD的解析式联立方程，解方程就可求出点D的坐标。
（3）抓住已知P点是抛物线上的动点且在第一象限，因此过点P作PN⊥x轴于点N，设P（x，﹣x2+2x+3），用含x的代数式分别表示出ON、PN、BN的长，再根据S△ABP=S梯形PNOA+S△PNB﹣S△AOB建立s与x的函数解析式，求出其顶点坐标，即可得出结果。
【考点精析】认真审题，首先需要了解确定一次函数的表达式(确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法)，还要掌握二次函数的最值(如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当x=-b/2a时，y最值=(4ac-b2)/4a)的相关知识才是答题的关键．