Question

【题目】已知：线段AB=40cm.

(1)如图①，点P沿线段AB自点A向点B以3厘米/秒运动，同时点Q线段BA自B点向点A以5厘米/秒运动，问经过几秒后P、Q相遇？

(2)几秒钟后，P、Q相距16厘米？

(3)如图②，AO=PO=8厘米，∠POB=40°，点P绕点O以20度/秒的速度顺时针旋转一周停止，同时点Q沿直线BA自B点向点A运动，假若P、Q两点能相遇，求Q运动的速度.

Answer 1

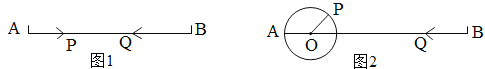
【答案】(1)经过5秒钟后P、Q相遇；(2)经过3秒钟或7秒钟后，P、Q相距16cm；(3)点Q运动的速度为12cm/s或cm/s.

【解析】

（1）根据相遇时，点P和点Q的运动的路程和等于AB的长列方程即可求解；
（2）设经过xs，P、Q两点相距10cm，分相遇前和相遇后两种情况建立方程求出其解即可；
（3）由于点P，Q只能在直线AB上相遇，而点P旋转到直线AB上的时间分两种情况，所以根据题意列出方程分别求解．

(1)设经过ts后，点P、Q相遇,

依题意，有3t+5t=40，

解得t=5.

答：经过5秒钟后P、Q相遇；

(2)设经过xs，P、Q两点相距16cm，由题意得

3x+5x+16=40或3x+5x16=40，

解得：x=3或x=7.

答：经过3秒钟或7秒钟后，P、Q相距16cm；

(3)点P，Q只能在直线AB上相遇，

则点P旋转到直线AB上的时间为40÷20=2s或(40+180)÷20=11s.

设点Q的速度为ycm/s,则有2y=4016,解得y=12或11y=40,解得

答：点Q运动的速度为12cm/s或cm/s.