
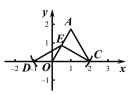
����Ŀ����ͼ1��E�ǵȱ�������ABC�ı�AB����ֱ����һ�㣬D�DZ�BC����ֱ����һ�㣬��D��C���غϣ���EC��ED�����DΪ��C���ڵȱ�������ABC�ķ��Ƶ㣬��E��Ϊ�������ģ�
��ƽ��ֱ������ϵxOy�У�
��1����֪�ȱ�������AOC�Ķ���C������Ϊ��2��0������A�ڵ�һ�����ڣ���������E��ֱ��AO�ϣ����Ƶ�D��ֱ��OC�ϣ�
����ͼ2����EΪ��AO���е㣬��ͼ��������C���ڵȱ�������AOC�ķ��Ƶ�D����ֱ��д����D�����꣺�� ����
����AE��2�����C���ڵȱ�������AOC�ķ��Ƶ�D�����ꣻ
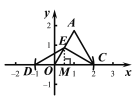
��2�����ȱ�������ABC�Ķ���ΪB��n��0����C��n+1��0������������E��ֱ��AB�ϣ����Ƶ�D��ֱ��BC�ϣ���2��AE��3����ֱ��д����C���ڵȱ�������ABC�ķ��Ƶ�D�ĺ�����t��ȡֵ��Χ���� �����ú�n�Ĵ���ʽ��ʾ����

���𰸡�(1)��D��-1,0��; ��D(![]() 2,0);(2)
2,0);(2) ![]() ��
��![]()
��������
��1���ٸ������з��Ƶ��뷴�����ĵĶ���������D���ɵ����ꣻ
����AO=OC=2����AE=2,��E����������ܵ�λ�ã���ͼ3��ͼ4�����ۣ��ɵ�D���ֵ��
(2)�ɣ�1���ɵ÷��Ƶ��뷴�����ĵĹ��ɣ���B(n,0)��C(n+1,0)��2��AE<3�ɵ�![]() ��
��![]() .
.
��1���� ��ͼ��
 ��
�� 
D(-1,0)
�� �ߵȱ�������AOC����������ΪO(0,0)��C(2,0),
��OC=2.
��AO=OC=2.
��AE=2��֪����E���������ܵ�λ�ã���ͼ3��ͼ4��.
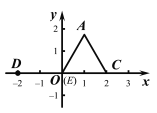

ͼ3 ͼ4
(��) ��ͼ3����E������ԭ��O�غ�.
��EC=ED��EC=2,
��ED=2.
��D�DZ�OC����ֱ����һ�㣬��D��C���غ�,
��D������Ϊ(![]() 2,0) .
2,0) .
(��) ��ͼ4����E�ڱ�OA���ӳ����ϣ���AE=2.
��AC=AE=2,
���E=��ACE.
�ߡ�AOCΪ�ȱ�������,
���OAC =��ACO=60��.
���E=��ACE=30��.
���OCE=90��.
��EC=ED,
���D���C�غ�.
������Ŀ�����е�D��C���غ�ì�ܣ�����ͼ4�е����������Ҫ����ȥ.
����������D(![]() 2,0). ��
2,0). ��
��2��![]() ��
��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������y= ![]() ��k��0����һ�κ���y=kx+k��k��0����ͬһƽ��ֱ������ϵ�ڵ�ͼ������ǣ� ��
��k��0����һ�κ���y=kx+k��k��0����ͬһƽ��ֱ������ϵ�ڵ�ͼ������ǣ� ��
A.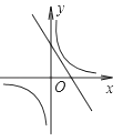
B.
C.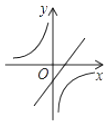
D.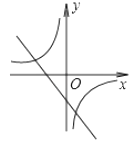
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������
��1��3x3x9��2xx3x8
��2����12+20160+��![]() ��2017������4��2018
��2017������4��2018
��3����x+4����x��4������x��2��2
��4��ab��a+b������a��b����a2+b2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2012��6��1���𣬹���ʵʩ�����������������֧�ָ�Ч���ܵ������ƹ�ʹ�ã�ij��ٿյ�������ʵʩ��ÿ����һ̨���ͻ��ɻ��������200Ԫ����ͬ����11��Ԫ������Ĵ˿�յ���̨������ʵʩ���ʵʩǰ��10%��������ʵʩǰ�˿�յ��ĵ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�ڣ���![]() Ϊ����ԭ�㣬��
Ϊ����ԭ�㣬��![]() ��
��![]() ���������ϣ���
���������ϣ���![]() ��
��![]() ��ĸ������ϣ���
��ĸ������ϣ���![]() ��
��![]() ���������ϣ�
���������ϣ�![]() ������
������![]() �����Ϊ
�����Ϊ![]() ��
��![]() ��
��![]() .
.
��1�����![]() ��
��![]() �����ꣻ
�����ꣻ
��2����![]() �ӵ�
�ӵ�![]() ������
������![]() ����λ/����ٶ���
����λ/����ٶ���![]() ���յ�
���յ�![]() �˶���ͬʱ����
�˶���ͬʱ����![]() �ӵ�
�ӵ�![]() ������
������![]() ����λ����ٶ���
����λ����ٶ���![]() ���յ�
���յ�![]() �˶������
�˶������![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ���߶�
���߶�![]() �ij�Ϊ
�ij�Ϊ![]() ���ú�
���ú�![]() �Ĺ�ϵʽ��ʾ
�Ĺ�ϵʽ��ʾ![]() ����ֱ��д����Ӧ��
����ֱ��д����Ӧ��![]() ��Χ.
��Χ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)��ͼ1���ѡ�ABC��DE�۵���ʹ��A���ڵ�A��������̽����1+��2���A�Ĺ�ϵ����֤������
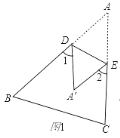
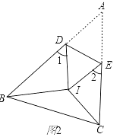
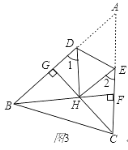
(2)��ͼ2��BIƽ�֡�ABC��CIƽ�֡�ACB���ѡ�ABC�۵���ʹ��A���I�غϣ�����1+��2=130�㣬���BIC�Ķ�����
(3)��ͼ3������ǡ�ABC�У�BF��AC�ڵ�F��CG��AB�ڵ�G��BF��CG���ڵ�H���ѡ�ABC�۵�ʹ��A�͵�H�غϣ���̽����BHC���1+��2�Ĺ�ϵ����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ��ѧϰ�˷�ʽ���̵Ľⷨ�������Ǿ���ͬѧ�Ľ�����̣�
�ⷽ�� ![]()
�⣺�������ã� ![]() ���������������������ڢٲ�
���������������������ڢٲ�
ȥ��ĸ���ã� ![]() ���������������������ڢڲ�
���������������������ڢڲ�
����ã� ![]() ������������������ �ڢ۲�
������������������ �ڢ۲�
�ϲ�ͬ����ã� ![]() ������������������ �ڢܲ�
������������������ �ڢܲ�
ϵ����1���ã� ![]() ���������������������ڢݲ�
���������������������ڢݲ�
���飺��![]() ʱ��
ʱ��![]()
����ԭ���̵Ľ���![]() �� �������������������ڢ�
�� �������������������ڢ�
���������Ľ�����̴ӵ�_____����ʼ���ִ������ԭ����_________________������ᄃ����������д�������Ľ�����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
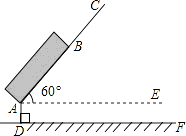
����Ŀ����ͼ�Ǵ����ڼ��һ���ؼҳ�����һ������ʽ�������ʾ��ͼ��ͼ��ʾ�����峤AB=50cm����������쳤����BC=30cm����A������ľ���AD=8cm����������ˮƽ��AE��60��ǣ������˰��ִ�C������ľ��루��ȷ��1cm�������ο����ݣ� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������У�ÿ��С�����εı߳���Ϊ1����λ���ȣ���ABC�����������λ����ͼ��ʾ���ֽ���ABCƽ�ƺ�á�DEF��ʹ��A�Ķ�Ӧ��Ϊ��D����B�Ķ�Ӧ��Ϊ��E��
��1��������DEF��
��2������AD��BE�����߶�AD��BE�Ĺ�ϵ�� ��
��3�����DEF�������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com