
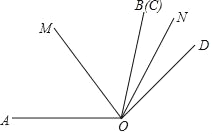
ЁОЬтФПЁПШчЭМЃЌЁЯAOBЃНІСЃЌЁЯCODЃНІТЃЈІСЃОІТЃЉЃЌOCгыOBжиКЯЃЌODдкЁЯAOBЭтЃЌЩфЯпOMЁЂONЗжБ№ЪЧЁЯAOCЁЂЁЯBODЕФНЧЦНЗжЯпЃЎ
ЃЈ1ЃЉЂйШєІСЃН100ЁуЃЌІТЃН60ЁуЃЌдђЁЯMONЕШгкЖрЩйЃЛ
ЂкдкЂйЕФЬѕМўЯТЁЯCODШЦЕуOФцЪБеыа§зЊnЁуЃЈ0ЃМnЃМ100ЃЈЧвnЁй60ЃЉЪБЃЌЧѓЁЯMONЕФЖШЪ§ЃЛ
ЃЈ2ЃЉжБНгаДГіЁЯCODШЦЕуOФцЪБеыа§зЊnЁуЃЈ0ЃМnЃМ360ЃЉЪБЁЯMONЕФжЕЃЈгУКЌІСЁЂІТЕФЪНзгБэЪОЃЉЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂйЁЯMONЃН80ЁуЃЛЂкЁЯMONЃН80ЁуЃЛЃЈ2ЃЉЁЯMONЃН![]() ЃЈІС+ІТЃЉЛђ180ЁуЉ
ЃЈІС+ІТЃЉЛђ180ЁуЉ![]() ЃЈІС+ІТЃЉЃЎ
ЃЈІС+ІТЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЂйИљОнНЧЦНЗжЯпЕФЖЈвхЧѓГіЁЯBOMКЭЁЯCONЕФЖШЪ§ЃЌШЛКѓЯрМгМДПЩЕУГіД№АИЃЛ
ЂкИљОна§зЊЕФаджЪПЩжЊЁЯBOC=nЁуЃЌЗжСНжжЧщПіНјааЬжТлЃКШчЭМ1ЃЌЁЯBODЃН60ЁуЉnЁуЃЌЁЯAOCЃН100ЁуЉnЁуЃЌИљОнНЧЦНЗжЯпЕФЖЈвхЕУГіЁЯCOMКЭЁЯBONЕФЖШЪ§ЃЌШЛКѓИљОнЁЯMONЃНЁЯCOM+ЁЯCOB+ЁЯBONНјааМЦЫуМДПЩЕУГіНсТлЃЛШчЭМ2ЃЌЁЯBODЃНnЁуЉ60ЁуЃЌЁЯAOCЃН100ЁуЉnЁуЃЌИљОнНЧЦНЗжЯпЕФЖЈвхЕУГіЁЯCOMКЭЁЯBONЕФЖШЪ§ЃЌШЛКѓИљОнЁЯMONЃНЁЯCOM+ЁЯCOD+ЁЯBONНјааМЦЫуМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉИљОнЂйЁЂЂкЕФНтЬтЫМТЗМДПЩЕУЕННсТлЃЎ
ЃЈ1ЃЉЂйЁпOMЃЌONЗжБ№ЪЧЁЯAOCЃЌЁЯBODЕФНЧЦНЗжЯпЃЌ
ЁрЁЯBOMЃН![]() ЁЯAOBЃЌЁЯBONЃН
ЁЯAOBЃЌЁЯBONЃН![]() ЁЯBODЃЌ
ЁЯBODЃЌ
ЁрЁЯMONЃН![]() ЃЈЁЯAOB+ЁЯBODЃЉЃЌ
ЃЈЁЯAOB+ЁЯBODЃЉЃЌ
гжЁпЁЯAOBЃН100ЁуЃЌЁЯCODЃН60ЁуЃЌ
ЁрЁЯMONЃН![]() ЃЈЁЯAOB+ЁЯBODЃЉЃН
ЃЈЁЯAOB+ЁЯBODЃЉЃН![]() ЁСЃЈ100Ёу+60ЁуЃЉЃН80ЁуЃЎ
ЁСЃЈ100Ёу+60ЁуЃЉЃН80ЁуЃЎ
ЂкШчЭМ1ЃЌЁпЁЯCODШЦЕуOФцЪБеыа§зЊnЁуЃЌ
ЁрЁЯBOCЃНnЁуЃЌ
ЁрЁЯBODЃН60ЁуЉnЁуЃЌЁЯAOCЃН100ЁуЉnЁуЃЌ
ЁпOMЃЌONЗжБ№ЪЧЁЯAOCЃЌЁЯBODЕФНЧЦНЗжЯпЃЌ
ЁрЁЯCOMЃН![]() ЁЯAOCЃН50ЁуЉ
ЁЯAOCЃН50ЁуЉ![]() nЁуЃЌЁЯBONЃН
nЁуЃЌЁЯBONЃН![]() ЁЯBODЃН30ЁуЉ
ЁЯBODЃН30ЁуЉ![]() nЁуЃЌ
nЁуЃЌ
ЁрЁЯMONЃНЁЯCOM+ЁЯCOB+ЁЯBONЃН80ЁуЃЛ
ШчЭМ2ЃЌЁпЁЯCODШЦЕуOФцЪБеыа§зЊnЁуЃЌ
ЁрЁЯBOCЃНnЁуЃЌ
ЁрЁЯBODЃНnЁуЉ60ЁуЃЌЁЯAOCЃН100ЁуЉnЁуЃЌ
ЁпOMЃЌONЗжБ№ЪЧЁЯAOCЃЌЁЯBODЕФНЧЦНЗжЯпЃЌ
ЁрЁЯCOMЃН![]() ЁЯAOCЃН50ЁуЉ
ЁЯAOCЃН50ЁуЉ![]() nЁуЃЌЁЯDONЃН
nЁуЃЌЁЯDONЃН![]() ЁЯBODЃН
ЁЯBODЃН![]() nЁуЉ30ЁуЃЌ
nЁуЉ30ЁуЃЌ
ЁрЁЯMONЃНЁЯCOM+ЁЯCOD+ЁЯDONЃН80ЁуЃЛ
ЃЈ2ЃЉЁпOMЮЊЁЯAODЕФЦНЗжЯпЃЌONЮЊЁЯBOCЕФЦНЗжЯпЃЌЁЯAOBЃНІСЃЌЁЯCODЃНІТЃЌ
ЁрЁЯMONЃН![]() ЃЈІС+ІТЃЉЛђ180ЁуЉ
ЃЈІС+ІТЃЉЛђ180ЁуЉ![]() ЃЈІС+ІТЃЉЃЛ
ЃЈІС+ІТЃЉЃЛ



 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПКЏЪ§y=kx+kЃЌгыy= ![]() дкЭЌвЛзјБъЯЕжаЕФЭМЯѓДѓжТШчЭМЃЌдђЃЈ ЃЉ
дкЭЌвЛзјБъЯЕжаЕФЭМЯѓДѓжТШчЭМЃЌдђЃЈ ЃЉ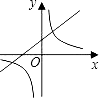
A.KЉ0
B.KЉ0
C.-1ЉKЉ0
D.KЉ-1
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌAЁЂBЁЂCЮЊЁбOЩЯЕФШ§ИіЕуЃЌЁбOЕФжБОЖЮЊ4cmЃЌЁЯACB=45ЁуЃЌЧѓABЕФГЄ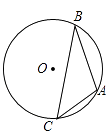
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯШЛЏМђЃЌдйЧѓжЕЃКa+![]() ЃЌЦфжаa=1007.ШчЭМЪЧаЁССКЭаЁЗМЕФНтД№Й§ГЬ.
ЃЌЦфжаa=1007.ШчЭМЪЧаЁССКЭаЁЗМЕФНтД№Й§ГЬ.
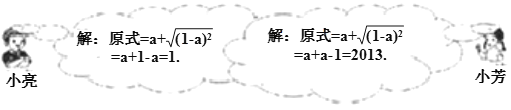
(1)_________ЕФНтЗЈЪЧДэЮѓЕФЃЛ
(2)ДэЮѓЕФдвђдкгкЮДФме§ШЗЕидЫгУЖўДЮИљЪНЕФаджЪЃК_________ЃЛ
(3)ЯШЛЏМђЃЌдйЧѓжЕЃКa+2![]() ЃЌЦфжаa=-2007.
ЃЌЦфжаa=-2007.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвЙњУїДњжщЫуМвГЬДѓЮЛЕФУћжјЁЖжБжИЫуЗЈЭГзкЁЗРягавЛЕРжјУћЫуЬтЃКЁАвЛАйТјЭЗвЛАйЩЎЃЌДѓЩЎШ§ИіИќЮоељЃЌаЁЩЎШ§ШЫЗжвЛИіЃЌДѓаЁКЭЩаИїМИЖЁЃПЁБвтЫМЪЧЃКга100ИіКЭЩаЗж100ИіТјЭЗЃЌШчЙћДѓКЭЩа1ШЫЗж3ИіЃЌаЁКЭЩа3ШЫЗж1ИіЃЌе§КУЗжЭъЃЌЪдЮЪДѓЁЂаЁКЭЩаИїЖрЩйШЫЃПЩшДѓКЭЩагаxШЫЃЌвРЬтвтСаЗНГЬЕУЃЈЁЁЁЁЃЉ
A. ![]() +3ЃЈ100ЉxЃЉЃН100 B.
+3ЃЈ100ЉxЃЉЃН100 B. ![]() Љ3ЃЈ100ЉxЃЉЃН100
Љ3ЃЈ100ЉxЃЉЃН100
C. 3xЉ![]() ЃН100 D. 3x+
ЃН100 D. 3x+![]() ЃН100
ЃН100
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
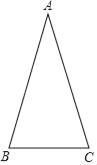
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAB=ACЃЌЕуDдкABБпЩЯЃЌЕуDЕНЕуAЕФОрРыгыЕуDЕНЕуCЕФОрРыЯрЕШЃЎ
ЃЈ1ЃЉРћгУГпЙцзїЭМзїГіЕуDЃЌВЛаДзїЗЈЕЋБЃСєзїЭМКлМЃЃЎ
ЃЈ2ЃЉШєЁїABCЕФЕзБпГЄ5ЃЌжмГЄЮЊ21ЃЌЧѓЁїBCDЕФжмГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫЙФРјЪаУёНкдМгУЫЎЃЌЮвЪаОгУёЪЙгУздРДЫЎМЦЗбЗНЪНЪЕЪЉНзЬнЫЎМлЃЌОпЬхБъзММћБэ1ЃЌБэ2ЗжБ№ЪЧаЁУїЁЂаЁРіЁЂаЁБѓЁЂаЁгюЫФМв2017ФъЕФФъгУЫЎСПКЭНЩФЩЫЎЗбЧщПіЃЎ
Бэ1ЃКДѓСЌЪаОгУёздРДЫЎЪЕЪЉНзЬнЫЎМлБъзМЧщПіЃК

Бэ2ЃКЫФИіМвЭЅ2017ФъЕФФъгУЫЎСПКЭНЩФЩЫЎЗбЧщПіЃК
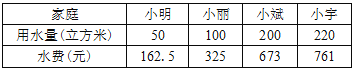
ЧыФуИљОнБэ1ЁЂБэ2ЬсЙЉЕФЪ§ОнЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉБэ1жаЕФ![]() __________ЃЌ
__________ЃЌ![]() _____________ЃЛ
_____________ЃЛ
ЃЈ2ЃЉаЁгБМв2017ФъЪЙгУздРДЫЎЙВНЩФЩЫЎЗб827дЊЃЌдђЫ§Мв2017ФъЕФФъгУЫЎСПЪЧЖрЩйСЂЗНУзЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌЕуCдкЁбOЩЯЃЌЁЯCABЕФЦНЗжЯпНЛЁбOгкЕуDЃЌЙ§ЕуDзїACЕФДЙЯпНЛACЕФбгГЄЯпгкЕуEЃЌСЌНгBCНЛADгкЕуFЃЎ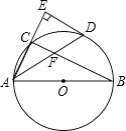
ЃЈ1ЃЉВТЯыEDгыЁбOЕФЮЛжУЙиЯЕЃЌВЂжЄУїФуЕФВТЯыЃЛ
ЃЈ2ЃЉШєAB=6ЃЌAD=5ЃЌЧѓAFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDжаЃЌAB=4cmЃЌЕуEЁЂFЭЌЪБДгCЕуГіЗЂЃЌвд1cm/sЕФЫйЖШЗжБ№биCBЉBAЁЂCDЉDAдЫЖЏЃЌЕНЕуAЪБЭЃжЙдЫЖЏЃЎЩшдЫЖЏЪБМфЮЊtЃЈsЃЉЃЌЁїAEFЕФУцЛ§ЮЊSЃЈcm2ЃЉЃЌдђSЃЈcm2ЃЉгыtЃЈsЃЉЕФКЏЪ§ЙиЯЕПЩгУЭМЯѓБэЪОЮЊЃЈ ЃЉ
A.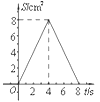
B.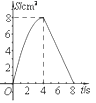
C.
D.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com