
【题目】如图所示,以平行四边形ABCD的顶点A为圆心,AB为半径作圆,分别交BC,AD于E,F两点,交BA的延长于G,判断弧EF和弧FG是否相等,并说明理由。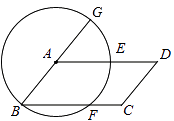
【答案】解:相等.
理由:连接AF.
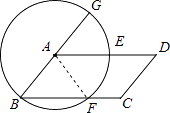
∵A为圆心,
∴AB=AF,
∴∠ABF=∠AFB,
∵四边形ABCD为平行四边形,
∴AD∥BC,∠AFB=∠DAF,∠GAD=∠ABF,
∴∠DAF=∠GAD,
∴ ![]() .
.
【解析】要证弧EF和弧FG相等,就需证这两条弧所对的圆心角相等。因此连接AF,根据已知的平行四边形得到AD∥BC,证明∠AFB=∠DAF,∠GAD=∠ABF,再根据等腰三角形的性质证明∠ABF=∠AFB,就可得出∠DAF=∠GAD,即可证得结论。
【考点精析】本题主要考查了平行线的性质和平行四边形的性质的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,O是AB上一点,以OA为半径的⊙O经过点D。
(1)求证:BC是⊙O切线;
(2)若BD=5,DC=3,求AC的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只箱子里共有3个球,其中2个白球,1个红球,它们除颜色外圴相同.
(1)从箱子里任意摸出一个球是白球的概率是多少?
(2)从箱子里任意摸出一个球,不将它放回,搅均后再摸出一球,求两次摸出的球都是白球的概率,并画出树状图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AD,BC是⊙O的两条互相垂直的直径,点P从点O出发沿图中某一个扇形顺时针匀速运动,设∠APB=y(单位:度),如果y与点P运动的时间x(单位:秒)的函数关系的图象大致如图2所示,那么点P的运动路线可能为( )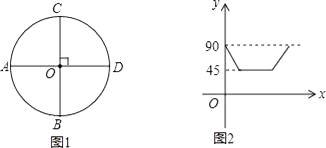
A.O→B→A→O
B.O→A→C→O
C.O→C→D→O
D.O→B→D→O
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值:a+![]() ,其中a=1007.如图是小亮和小芳的解答过程.
,其中a=1007.如图是小亮和小芳的解答过程.
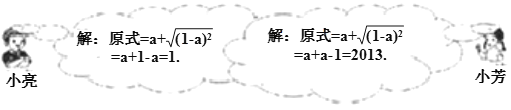
(1)_________的解法是错误的;
(2)错误的原因在于未能正确地运用二次根式的性质:_________;
(3)先化简,再求值:a+2![]() ,其中a=-2007.
,其中a=-2007.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D在AB边上,点D到点A的距离与点D到点C的距离相等.
(1)利用尺规作图作出点D,不写作法但保留作图痕迹.
(2)若△ABC的底边长5,周长为21,求△BCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
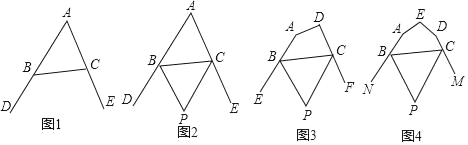
【题目】(1)如图1,在△ABC中,∠DBC与∠ECB分别为△ABC的两个外角,若∠A=60°,∠DBC+∠ECB多少度;
(2)如图2,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有怎样的数量关系?为什么?
(3)如图3,在四边形ABCD中,BP、CP分别平分外角∠EBC、∠FCB,∠P与∠A+∠D有怎样的数量关系?为什么?
(4)如图4,在五边形ABCDE中,BP、CP分别平分外角∠NBC、∠MCB,∠P与∠A+∠D+∠E有怎样的数量关系?(直接写出答案).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com