
【题目】如图,已知矩形纸片ABCD中,AB=12,BC=16.将矩形纸片ABCD折叠,使点B与点D重合,点A折叠至点E处,GH为折痕,连接BG.
(1)△DGH是等腰三角形吗?请说明你的理由.
(2)求线段AG的长;
(3)求折痕GH的长.

【答案】(1)△ DGH是等腰三角形,理由见解析;(2) AG=3.5;(3)折痕GH的长为15.
【解析】
(1)由翻折,找着重合的部分,得到相等的边,相等的角,再根据两直线平行,内错角相等可得即可证明;
(2)设出未知数,用未知数表示出相关的量,应用勾股定理,列出方程可求得答案.
(3)由(2)知BG=DG=16-3.5=12.5,因为 DG=DH=BH,GE∥DH,从而求出四边形BHDG是菱形,再利用勾股定理列式求出BD,然后根据菱形的面积列出方程求解即可.
(1)![]() DGH是等腰三角形,理由如下:在矩形ABCD中,∵AD∥BC,∴∠DGH=∠BHG,由折叠知∠DHG=∠BHG,∴∠DGH=∠DHG,∴DG=DH,即
DGH是等腰三角形,理由如下:在矩形ABCD中,∵AD∥BC,∴∠DGH=∠BHG,由折叠知∠DHG=∠BHG,∴∠DGH=∠DHG,∴DG=DH,即![]() DGH是等腰三角形;
DGH是等腰三角形;
(2)由折叠知AG=GE,设AG=x,则BG=DG=16-x,∵∠A=90°,![]() ,∴
,∴![]() ,解得x=3.5,∴AG=3.5;
,解得x=3.5,∴AG=3.5;
(3)由(2)知BG=DG=16-3.5=12.5,∵DG=DH=BH,GE∥DH,∴四边形BHDG是平行四边形,∴四边形BHDG是菱形.;
法一:作GF⊥BC于点F,则BF=AG=3.5,GF=AB=12,∴FH=BH-BF=12.5-3.5=9,
∴GH=![]() =
=![]() ,∴折痕GH的长为15.;
,∴折痕GH的长为15.;
法二:连接BD,则BD=![]() =
=![]() =20,∵四边形BHDG是菱形,
=20,∵四边形BHDG是菱形,
∴S菱形BHDG=BH·AB=![]() BD·GH,∴GH=
BD·GH,∴GH=![]() =15,∴折痕GH的长为15..
=15,∴折痕GH的长为15..


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】本学期学习了分式方程的解法,下面是晶晶同学的解题过程:
解方程 ![]()
解:整理,得: ![]() …………………………第①步
…………………………第①步
去分母,得: ![]() …………………………第②步
…………………………第②步
移项,得: ![]() ……………………… 第③步
……………………… 第③步
合并同类项,得: ![]() ……………………… 第④步
……………………… 第④步
系数化1,得: ![]() …………………………第⑤步
…………………………第⑤步
检验:当![]() 时,
时,![]()
所以原方程的解是![]() . ………………………第⑥步
. ………………………第⑥步
上述晶晶的解题过程从第_____步开始出现错误,错误的原因是_________________.请你帮晶晶改正错误,写出完整的解题过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长都为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移后得△DEF,使点A的对应点为点D,点B的对应点为点E.
(1)画出△DEF;
(2)连接AD、BE,则线段AD与BE的关系是 ;
(3)求△DEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据市卫生防疫部门的要求,游泳池必须定期换水后才能对外开放.在换水时需要经“排水—清冼—灌水”的过程.某游泳馆从早上7:00开始对游泳池进行换水,已知该游泳池的排水速度是灌水速度的1.6倍,其中游泳池内剩余的水量y(m3)与换水时间x(h)之间的函数图象如图所示,根据图象解答下列问题:
(1)填空:该游泳池清洗需要 小时;
(2)求排水过程中的y(m3)与x(h)之间的函数关系式,并写出自变量x的取值范围;
(3)若该游泳馆在换水结束后30分钟才能对外开放,试问游泳爱好者小明能否在中午12:40进入该游泳馆游泳?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸中,每个小正方形的边长为1个单位长度,△ABC的顶点都在格点上.

(1)画出△ABC先向右平移6格,再向上平移1格所得的△A′B′C′;
(2)画出△ABC的AB边上的中线CD和高线CE;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】麒麟区第七中学现有一块空地ABCD如图所示,现计划在空地上种草皮,经测量,∠B=90°,AB=3m,BC=4m,CD=13m,AD=12m.

(1)求出空地ABCD的面积?
(2)若每种植1平方米草皮需要300元,问总共需投入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“足球运球”是中考体育必考项目之一兰州市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.
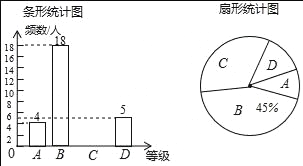
根据所给信息,解答以下问题
(1)本次一共抽取了 名九年级学生;
(2)补全条形统计图;
(3)在扇形统计图中,C对应的扇形的圆心角是 度;
(4)该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点C在AOB的一边OA上,过点C的直线DE//OB,CF平分ACD,CG CF于C .
(1)若O =40,求ECF的度数;
(2)求证:CG平分OCD;
(3)当O为多少度时,CD平分OCF,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com