
【题目】计算
(1)a×a3×(﹣a2)3
(2)(![]() )﹣1+(
)﹣1+(![]() )2×(﹣2)3﹣(π﹣3)0
)2×(﹣2)3﹣(π﹣3)0
(3)(﹣0.25)11×(﹣4)12
(4)(﹣2a2)2×a4﹣(﹣5a4)2.
(5)(x﹣y)6÷(y﹣x)3×(x﹣y)2
(6)314×(﹣![]() )7.
)7.
【答案】(1)﹣a10(2)0(3)-4(4)﹣21a8(5)﹣(x﹣y)11(6)-1
【解析】
试题分析:(1)根据幂的乘方和同底数幂的乘法进行计算即可;
(2)根据负整数指数幂、幂的乘方、零指数幂的计算方法进行计算即可;
(3)根据幂的乘方进行计算即可;
(4)根据积的乘方和同底数幂的乘法进行计算即可;
(5)根据同底数幂的乘法进行计算即可;
(6)根据同底数幂的乘法进行计算即可.
解:(1)a×a3×(﹣a2)3
=a×a3×(﹣a6)
=﹣a10;
(2)(![]() )﹣1+(
)﹣1+(![]() )2×(﹣2)3﹣(π﹣3)0
)2×(﹣2)3﹣(π﹣3)0
=![]()
=3﹣2﹣1
=0;
(3)(﹣0.25)11×(﹣4)12
=![]()
=﹣![]()
=﹣4;
(4)(﹣2a2)2×a4﹣(﹣5a4)2
=4a4×a4﹣25a8
=4a8﹣25a8
=﹣21a8;
(5)(x﹣y)6÷(y﹣x)3×(x﹣y)2
=﹣(x﹣y)6(x﹣y)3(x﹣y)2
=﹣(x﹣y)11;
(6)314×(﹣![]() )7
)7
=![]()
=![]()
=﹣1.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
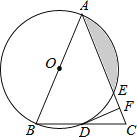
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】县医院住院部在连续10天测量某病人的体温与36℃的上下波动数据为:0.2, 0.3, 0.1, 0.1, 0, 0.2, 0.1, 0.1, 0.1, 0,则对这10天中该病人的体温波动数据分析不正确的是( )
A.平均数为0.12 B.众数为0.1
C.中位数为0.1 D.方差为0.02
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知∠AOB=α,在射线OA、OB上分别取点OA1=OB1,连结A1B1,在B1A1、B1B上分别取点A2、B2,使B1B2=B1A2,连结A2B2…按此规律下去,记∠A2B1 B2=θ1,∠A3B2B3=θ2,…,∠An+1Bn Bn+1=θn,则θ2016﹣θ2015的值为( )
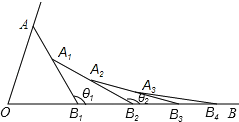
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某学校学生的个性特长发展情况,在全校范围内随机抽查了部分学生参加音乐、体育、美术、书法等活动项目(每人只限一项)的情况.并将所得数据进行了统计,结果如图所示.
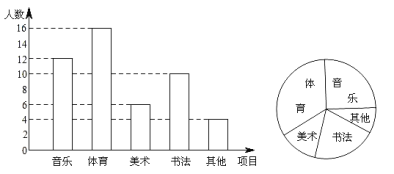
(1)求在这次调查中,一共抽查了多少名学生;
(2)求出扇形统计图中参加“音乐”活动项目所对扇形的圆心角的度数;
(3)若该校有2400名学生,请估计该校参加“美术”活动项目的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线OA∥射线CB,∠C=∠OAB=100°.点D、E在线段CB上,且∠DOB=∠BOA,OE平分∠DOC.
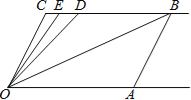
(1)试说明AB∥OC的理由;
(2)试求∠BOE的度数;
(3)平移线段AB;
①试问∠OBC:∠ODC的值是否会发生变化?若不会,请求出这个比值;若会,请找出相应变化规律.
②若在平移过程中存在某种情况使得∠OEC=∠OBA,试求此时∠OEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面内有直线a1,a2,a3,a4, …, a100,若a1⊥a2,a2∥a3,a3⊥a4,a4∥a5, …,按此规律进行下去,则a1与a100的位置关系是( )
A. 平行 B. 相交 C. 重合 D. 无法判断
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com